题意:告诉你n个01串长度总3e4,看你能否构造一个无限长的01一串使其任何子串都不包含这n个01串。
思路:可以用n个01串建立一个ac自动机,如果无限长的话,意思则就是能否在ac自动机上构造一个无限长的链条使得每一个fail和 fail的fail 和 fail的fail的fail…不包含被标记的结点。实际上我们只要在ac自动机上找到一个环便可构造无限长的链条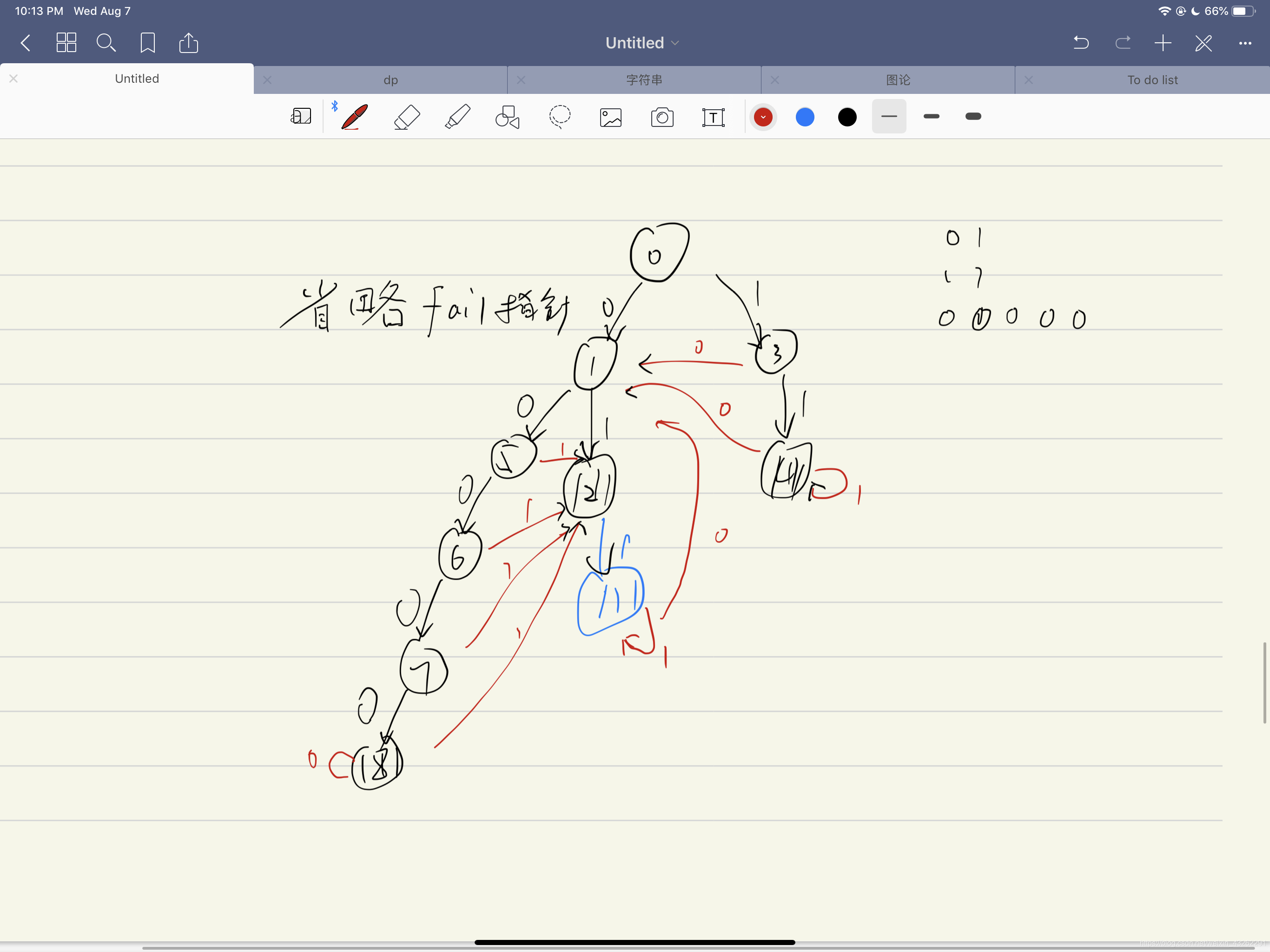
如图,如果是第一个串是01那么显然没有合法环,如果是011那么1 5 2便已经找到合法环了,它可以构造出001001001001001001…的无限串
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define forn(i,n) for(int i=0;i<n;i++)
#define for1(i,n) for(int i=1;i<=n;i++)
#define IO ios::sync_with_stdio(false);cin.tie(0);cout.tie(0)
const int maxn = 3e4+5;
int trie[maxn][2],id,flag[maxn],fail[maxn];
bool vis[maxn],viss[maxn];
class Aho{
public:
void insert(string s){
int len = s.size(),u = 0;
forn(i,len){
int x = s[i]-'0';
if(!trie[u][x]) trie[u][x] = ++id;
u = trie[u][x];
}
flag [u] = 1;
}
queue<int>q;
void build(){
forn(i,2) if(trie[0][i]) q.push(trie[0][i]);
while(!q.empty()){
int u = q.front();q.pop();
flag[u] |= flag[fail[u]];
forn(i,2){
if(trie[u][i]) fail[trie[u][i]] = trie[fail[u]][i],q.push(trie[u][i]);
else trie[u][i] = trie[fail[u]][i];
}
}
}
}aho;
bool dfs(int u){
vis[u] = 1;
forn(i,2){
int v = trie[u][i];
//if(vis[v]) cerr<<"@!!@#!@#"<<' '<<u<<' '<<i<<' '<<v<<'
';
if(vis[v]) return 1;
if(viss[v]||flag[v]) continue;
viss[v] = 1;
if(dfs(v)) return 1;
}
vis[u] = 0;
return 0;
}
int main(){
//IO;
int n;cin>>n;
string s;
forn(i,n){
cin>>s;
aho.insert(s);
}
aho.build();
if(dfs(0)) cout<<"TAK"<<'
';
else cout<<"NIE"<<'
';
return 0;
}