DFS树博客:链接
双连通是对无向图所说的
边双:对于一个图G,和子图G2,如果去除图中任意一个边子图G2仍然连通的话,G2中的边就是边双联通
- 关于边双点双桥割点的DFS做法
跟OIwiki学的:链接
对图跑出一颗DFS树。
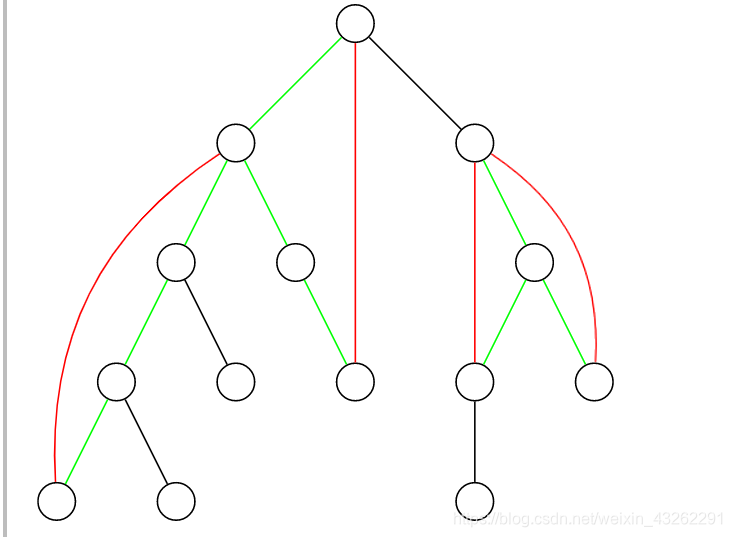
如图,图源OIwiki,黑边绿边为树边,红边为非树边。被红边所关照两点的树上路径必然不是桥,除此之外的就都是桥了,所以求桥的方法就是用差分。对于非树边u-v, 假设v为更深的树点,那么开个差分数组a[v]++, a[u]–;在DFS回溯的过程中差分,这样就标记好了。两点是否边双连通,就看树上路径是否有桥
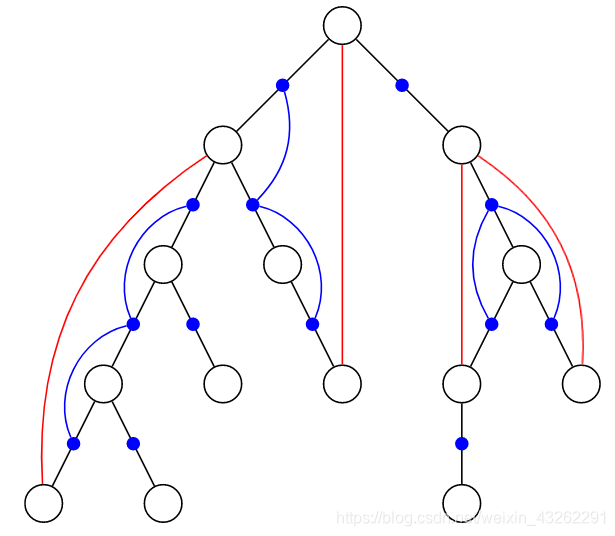
如下图,黑边为树边,红遍为非树边,将非树边两点所对应的树上路径加入一个联通块。这样如果一个点周边的所有的边都属于一个联通块,那么它不是割点,此外就是。点双连通,条件为两点间的路径上的边都为一个联通块。
2. Tarjan做法
A. 判断割点:
我们开两个数组一个为dfn时间戳代表我们dfs访问点的顺序,另一个为low,这个数组不知道该怎么定义,我觉得可以这样说,它所连接的路径直接返回时间戳最小值。对于判割点的算法应该是这样的,对于求scc的按板子定义吧。
这样的话一个点u直接相连的点v如果有一个不能返回到比dfn[u]小的时间戳,那么该点为割点,如果这个点是根节点的话,需要特判,当它的儿子数>=2的时候它也是割点。
例题1:洛谷P3388求哪些是割点
代码:
#include <bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0)
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
const int maxn = 2e4 + 5;
int ans, ind;
int dfn[maxn], low[maxn];
bool pcut[maxn];
vector<int>e[maxn],res;
inline void tarjan(int u, int pre) {
dfn[u] = low[u] = ++ind;
int son = 0;
for(auto v : e[u]) {
if(!dfn[v]) {
++son;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(u != pre && !pcut[u] && low[v] >= dfn[u]) {
pcut[u] = 1;
++ans;
res.push_back(u);
}
}else if(v != pre) low[u] = min(low[u], dfn[v]);
}
if(u == pre && !pcut[u] && son > 1) {
pcut[u] = 1;
++ans;
res.push_back(u);
}
}
int main() {
IO;
int n, m; cin >> n >> m;
forn(i, m) {
int u, v; cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
for1(i, n) if(!dfn[i]) tarjan(i, i);
cout << ans << '
';
sort(res.begin(), res.end());
for(auto x : res) cout << x << ' ';
return 0;
}
例题2:POJ2117求一个图删除一个点之后,联通块最多有多少。
#include<cstdio>
#include<iostream>
#include<algorithm>
#include<string>
#include<cstring>
#include<queue>
#include<stack>
#include<map>
#include<set>
#include<cmath>
#include<sstream>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0)
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
const int maxn = 1e4 + 5;
int ans, ind, ma;
int dfn[maxn], low[maxn], pcut[maxn];
vector<int>e[maxn];
inline void init(int n) {
ans = 0, ind = 0, ma = 0;
forn(i, n + 5) {
e[i].clear();
dfn[i] = pcut[i] = 0;
}
}
inline void tarjan(int u, int pre) {
dfn[u] = low[u] = ++ind;
int son = 0;
for(int i = 0; i < e[u].size(); ++i) {
int v = e[u][i];
if(!dfn[v]) {
++son;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(u != pre && low[v] >= dfn[u]) {
//cerr << "!@ " << u << ' '<< v << '
';
++pcut[u];
ma = max(ma, pcut[u]);
}
}else if(v != pre) low[u] = min(low[u], dfn[v]);
}
if(u == pre && son > 1) {
//cerr << "!@2 " << u << '
';
pcut[u] = son - 1;
ma = max(ma, pcut[u]);
}
}
int main() {
IO;
int n, m;while(cin >> n >> m && (n || m)) {
init(n);
forn(i, m) {
int u, v; cin >> u >> v;
++u, ++v;
e[u].push_back(v);
e[v].push_back(u);
}
for1(i, n) if(!dfn[i]) tarjan(i, i), ++ans;
ans += ma;
cout << min(ans, n - 1) << '
';
}
return 0;
}
B.求桥:
如果一条边所连的u点和v点,low[v] > dfn[u]那么代表此条边为桥。
例题1:HDU4738
代码:
#include <bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0)
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
const int inf = 2e9;
const int maxn = 1005;
vector<pair<int, int> >e[maxn];
int ind, mi = inf;
int val[maxn], dfn[maxn], low[maxn];
bool bri[maxn];
inline void init(int n) {
ind = 0, mi = inf;
for(int i = 0; i < n + 5; ++i) {
dfn[i] = bri[i] = 0;
e[i].clear();
}
}
inline void tarjan(int u, int pre) {
dfn[u] = low[u] = ++ind;
bool ok = 0;
for(auto &x : e[u]) {
int v = x.first, w = x.second;
val[v] = w;
if(!dfn[v]) {
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > dfn[u]) {
bri[v] = 1;
mi = min(mi, w);
}
}else {
if(v != pre) low[u] = min(low[u], dfn[v]);
else {
if(ok) low[u] = min(low[u], dfn[v]);
ok = 1;
}
}
}
}
int main() {
IO;
//freopen("in.txt", "r", stdin);
int n, m; while(cin >> n >> m && (n || m)) {
/*if(!m) {
cout << 0 << '
';
continue;
}*/
forn(i, m) {
int u, v, w;
cin >> u >> v >> w;
e[u].push_back({v, w});
e[v].push_back({u, w});
}
int cnt = 0;
for1(i, n) if(!dfn[i]) tarjan(i, i), ++cnt;
if(cnt > 1) cout << 0 << '
';
else if(mi == inf) cout << -1 << '
';
else cout << max(mi, 1) << '
';
init(n);
}
return 0;
}
例题2:HDU2460 一张图,m次操作,每次操作在u, v间添加一条边,然后当前图中桥个数
思路:很显然和上面将的DFS一样,u,v加一条边会使得u v树上路径的所以边变为非桥边。利用跟并查集类似的做法就可以做到线性复杂度了。
代码:
#include <bits/stdc++.h>
using namespace std;
#define IO ios::sync_with_stdio(false);cin.tie(0)
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
#pragma comment(linker,"/STACk:10240000,10240000")
const int maxn = 1e5 + 5;
vector<int>e[maxn];
bool bri[maxn];
int n, m, ans, ind;
int dfn[maxn], low[maxn], fa[maxn], deep[maxn], par[maxn];
inline void init(int n) {
ans = ind = 0;
forn(i, n + 5) {
e[i].clear();
fa[i] = deep[i] = dfn[i] = bri[i] = 0;
par[i] = i;
}
}
inline void tarjan(int u, int pre, int d) {
bool ok = 0;
fa[u] = pre, deep[u] = d;
dfn[u] = low[u] = ++ind;
for(auto v : e[u]) {
if(!dfn[v]) {
tarjan(v, u, d + 1);
low[u] = min(low[u], low[v]);
if(!bri[v] && low[v] > dfn[u]) {
++ans;
bri[v] = 1;
}
}else {
if(v != pre) low[u] = min(low[u], dfn[v]);
else {
if(ok) low[u] = min(low[u], dfn[v]);
ok = 1;
}
}
}
}
inline int find(int x) {
return x == par[x] ? x : par[x] = find(par[x]);
}
inline void change(int u, int v) {
u = find(u), v = find(v);
//cerr << "!@# " << u << ' ' << v << '
';
if(u == v) return;
vector<int>tmp;
while(u != v) {
if(bri[u]) bri[u] = 0, --ans;
if(bri[v]) bri[v] = 0, --ans;
if(deep[u] > deep[v]) {
tmp.push_back(u);
u = fa[u], u = par[u];
}else if(deep[u] < deep[v]) {
tmp.push_back(v);
v = fa[v], v = par[v];
}else {
tmp.push_back(u);
tmp.push_back(v);
u = fa[u], u = par[u];
v = fa[v], v = par[v];
}
}
for(auto x : tmp) par[x] = u;
}
int main() {
//freopen("in.txt", "r", stdin);
IO;
int T = 0;
forn(i, maxn) par[i] = i;
while(cin >> n >> m && (n || m)) {
++T;
forn(i, m) {
int u, v; cin >> u >> v;
e[u].push_back(v);
e[v].push_back(u);
}
tarjan(1, 1, 1);
cout << "Case " << T << ":
";
int q; cin >> q;
while(q--) {
int u, v; cin >> u >> v;
change(u, v);
cout << ans << '
';
if(!q) cout << '
';
}
init(n);
}
return 0;
}
C. 求双联通块:
在DFS的过程中开个栈,存下DFS访问的点。
当low[v] >= dfn[u],也就是对u造成割点判断的时候,就分一个双联通块,然后把Stack 吐到u-v这条边。
例题:
洛谷P3225 (WF2011的一题)在一个无向图上选择尽量少的点涂黑,使得任意删除一个点后,每个连通分量至少有一个 黑点。去最小黑点数和满足黑点数的方案数。
做法:
不能涂到割点,因为割点没了,它所分开的联通块都没有黑点。
对于一个双连通块,涂除割点以外的点。但是如果一个双联通块有两个割点,那么他就不需要涂了,因为它总能链接到其他双联通块。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
#define IO ios::sync_with_stdio(false);cin.tie(0)
const int maxn = 505;
struct edge {
int v, nex;
}e[maxn << 1];
bool pcut[maxn << 1];
int tot, id, cnt;
pair<int, int> a[maxn];
int head[maxn << 1], dfn[maxn << 1], low[maxn << 1], color[maxn << 1];
vector<int> bcc[maxn << 1];
stack<pair<int, int> > s;
inline void add(int u, int v) {
e[++tot] = {v, head[u]}, head[u] = tot;
e[++tot] = {u, head[v]}, head[v] = tot;
}
inline void init() {
tot = id = cnt = 0;
forn(i, maxn << 1) {
head[i] = dfn[i] = pcut[i] = color[i] = 0;
bcc[i].clear();
}
while(!s.empty()) s.pop();
}
inline void tarjan(int u, int pre) {
dfn[u] = low[u] = ++id;
int son = 0;
for(int i = head[u]; i; i = e[i].nex) {
int v = e[i].v;
if(!dfn[v]) {
s.push({u, v});
++son;
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] >= dfn[u]) {
pcut[u] = 1;
++cnt;
while(1) {
auto now = s.top(); s.pop();
int x = now.first, y = now.second;
if(color[x] != cnt) bcc[cnt].push_back(x), color[x] = cnt;
if(color[y] != cnt) bcc[cnt].push_back(y), color[y] = cnt;
if(x == u && y == v) break;
}
}
}else if(v != pre && dfn[v] < dfn[u]) {
low[u] = min(low[u], dfn[v]);
s.push({u, v});
}
}
if(u == pre && son <= 1) pcut[u] = 0;
}
int main() {
//freopen("a.txt", "w", stdout);
IO;
int n, T = 0; while(cin >> n && n) {
++T;
vector<int> has;
for1(i, n) {
cin >> a[i].first >> a[i].second;
has.push_back(a[i].first);
has.push_back(a[i].second);
}
sort(has.begin(), has.end());
has.erase(unique(has.begin(), has.end()) , has.end());
for1(i, n) {
int u = lower_bound(has.begin(), has.end(), a[i].first) - has.begin() + 1;
int v = lower_bound(has.begin(), has.end(), a[i].second) - has.begin() + 1;
a[i].first = u, a[i].second = v;
add(u, v);
}
for(auto x : has) {
if(!dfn[x]) tarjan(x, x);
}
ll ans1 = 0, ans2 = 1;
for1(i, cnt) {
int cntt = 0;
//cout << "@!#@! " << i << '
';
for(auto x : bcc[i]) {
if(pcut[x]) ++cntt;
//cout << x << ' ' << pcut[x] << ' ';
}
if(cntt == 1) {
++ans1;
ans2 *= bcc[i].size() - 1;
}
//cout << '
';
}
if(cnt == 1) ans1 = 2, ans2 = bcc[1].size() * (bcc[1].size() - 1) / 2;
cout << "Case " << T << ": ";
cout << ans1 << ' ' << ans2 << '
';
init();
}
return 0;
}
D. 求边双连通
把桥边摘出来,剩下的边跑有几个联通块,每个联通块就是边双。
例题:2019 Yokohama Regional I题(日本区金牌题)
给一个无向图,n个人第i个人从ai点走到bi点,现在让给无向图定向,使得每个人都能通过有向边从ai走到bi。
是否有解,输出方案。
做法:
对边双,DFS树上的边正向,非树边反向。剩下的桥所相连着两个边双,我们把边双缩点。缩点后的图是棵树,边都是桥。
然后对着这个图去跑询问,如果ai 和 bi不在新图的一个联通块,不可能达到。此外找到ai 和 bi的lca,对3点做差分,开两个差分数组,一个数组表示边方向逆树访问方向,另一个数组表示边方向顺树访问方向。然后差分如果两个数组同时有值就代表不可能。
代码:
#include <bits/stdc++.h>
using namespace std;
#define ll long long
#define forn(i, n) for(int i = 0; i < n; ++i)
#define for1(i, n) for(int i = 1; i <= n; ++i)
#define IO ios::sync_with_stdio(false);cin.tie(0)
const int maxn = 1e4 + 5;
const int maxm = 1e5 + 5;
vector<pair<int,int> >G[maxn];
struct edage{
int u, v, nex;
}e[maxm << 1];
int tim, tot = 1, bccnt, sccnt;
int dfn[maxn], low[maxn], Dp[maxn], head[maxn], bcc[maxn], scc[maxn], fa[maxn][20], deep[maxn], st[maxn], ed[maxn], pp[maxn], a[maxn], b[maxn];
bool bri[maxm << 1], ok[maxm << 1], vis[maxn];
inline void add(int u, int v) {
e[++tot] = {u, v, head[u]}, head[u] = tot;
e[++tot] = {v, u, head[v]}, head[v] = tot;
}
inline void tarjan(int u, int pre) {
dfn[u] = low[u] = ++tim;
for(int i = head[u]; i; i = e[i].nex) {
int v = e[i].v;
if(v == pre) continue;
if(!dfn[v]) {
tarjan(v, u);
low[u] = min(low[u], low[v]);
if(low[v] > dfn[u]) bri[i] = bri[i ^ 1] = 1;
}else low[u] = min(low[u], dfn[v]);
}
}
inline void dfs(int u, int pre, int d) {
bcc[u] = bccnt, Dp[u] = d;
for(int i = head[u]; i; i = e[i].nex) {
int v = e[i].v;
if(v == pre) continue;
if(bri[i]) continue;
if(!bcc[v]) {
ok[i] = 1;
dfs(v, u, d + 1);
}else if(Dp[u] > Dp[v])ok[i] = 1;
}
}
inline void dfs2(int u, int pre, int d) {
scc[u] = sccnt, deep[u] = d, fa[u][0] = pre;
for(int i = 1; deep[u] - (1 << i) >= 0; ++i) {
fa[u][i] = fa[fa[u][i - 1]][i - 1];
}
for(auto &x : G[u]) {
int v = x.first;
if(scc[v]) continue;
pp[v] = x.second;
dfs2(v, u, d + 1);
}
}
inline int LCA(int u, int v) {
if(deep[u] < deep[v]) swap(u, v);
for(int i = 14; i >= 0; --i) {
if(deep[fa[u][i]] >= deep[v]) {
u = fa[u][i];
}
}
if(u == v) return u;
for(int i = 14; i >= 0; --i) {
if(fa[u][i] != fa[v][i]) u = fa[u][i], v = fa[v][i];
}
return fa[u][0];
}
inline void getans(int u) {
vis[u] = 1;
a[u] = st[u], b[u] = ed[u];
for(auto &x : G[u]) {
int v = x.first;
if(vis[v]) continue;
getans(v);
a[u] += a[v], b[u] += b[v];
}
if(a[u] && b[u]) {
cout << "No" << '
';
exit(0);
}
else if(a[u]) ok[pp[u] ^ 1] = 1;
else ok[pp[u]] = 1;
}
int main() {
IO;
int n, m; cin >> n >> m;
forn(i, m) {
int u, v; cin >> u >> v;
add(u, v);
}
for1(i, n) if(!dfn[i]) tarjan(i, i);
for1(i, n) if(!bcc[i]) ++bccnt, dfs(i, i, 1);
for(int i = 2; i <= tot; ++i) if(bri[i]) {
int u = bcc[e[i].u], v = bcc[e[i].v];
G[u].push_back({v, i});
}
vector<int> root;
for1(i, bccnt) if(!scc[i]) ++sccnt, dfs2(i, i, 1), root.push_back(i);
int q; cin >> q;
forn(i, q) {
int u, v; cin >> u >> v;
u = bcc[u], v = bcc[v];
int lca = LCA(u, v);
if(scc[u] != scc[v]) return cout <<"No
", 0;
++st[u], --st[lca];
++ed[v], --ed[lca];
}
for(auto x : root) getans(x);
cout << "Yes" << '
';
for(int i = 2; i <= tot; ++i) {
if(!ok[i]) continue;
cout << e[i].u << ' ' << e[i].v << '
';
}
return 0;
}