《算法竞赛入门经典》计算组合数问题

计算组合数

编写函数，参数是两个非负整数n和m，返回组合数

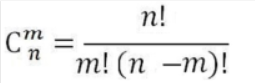
其中m<=n<=25。例如，n=25,m=12时的答案为5200300。

代码及算法分析

程序4-1 组合数（有问题）

#include <stdio.h>
long long factorial(int n)
{
 long long m=1;
 //不要忘记初始化，不然的出来的结果惊人。
 for(int i=1;i<=n;i++)
 {
  m*=i;
 }
 return m;
}
int main ()
{
 int n,m;
 scanf("%d %d",&n,&m);
 printf("%lld",factorial(n)/(factorial(m)*factorial(n-m)));
 return 0;
}

这个代码的问题显而易见，阶乘容易溢出，所以不可取。
所以，套用刘汝佳老师的一句话：”即使最终答案在所选择的数据类型范围之内，计算的中间结果仍然可能溢出“。

汝佳老师也给出了相应的解决方案，虽然不能完全避免中间结果溢出，但是对于题目给出的范围已经可以保证得到正确的结果了。
先来分析一下组合数的公式：
n!
————
m!(n-m)!
展开之后：
n *(n-1) *(n-2)……3 *2 *1
—————————————————————————————（1）
m *(m-1) *(m-2)……3 *2 *1 *(n-m) *(n-m-1) *(n-m-2)…… *3 *2 *1
因为n>=m，所以m在1~n之间，这样可以把n!除以m!约分：
n *(n-1) *(n-2)……(m+2) *(m+1)
————————————————（2）
(n-m) *(n-m-1) *(n-m-2)…… *3 *2 *1

然后汝佳老师给了一道思考题：为什么当m<n-m时要把m变成n-m？
移项之后得到：m<n/2，先列一个数轴：
|————————————————————>
0 1 2 3 ……m……n/2……M……(n-1) n
为了不把变换后的m与变换前的m弄混，把变化后的m记为M。因为组合数的公式，分子是大于分母的，所以分子的乘积比较大，容易溢出，要想优化，就得让分子乘积变小。
M=n-m带入组合式公式之后就是：
n!
————————————————（3）
M!(n-M)!=(n-m)!(n-(n-m))!=(n-m)!m!
所以式子并没有变化，同样可以进行约分得到（2）式的变式：
n *(n-1) *(n-2)……(M+2) *(M+1)
————————————————（4）
(n-M) *(n-M-1) *(n-M-2)…… *3 *2 *1
相当于将数轴
|————————————————————>
0 1 2 3 ……m ……n/2……M ……(n-1) n
标出的部分直接干掉了。

由于M是大于m的，所以分子的乘积缩小，溢出问题得到缓解，注意，是缓解不是解决，如果n和m的值很大的话还是会溢出。
分析之后就可以把程序4-1升级为程序4-2了：

#include <stdio.h>
long long c(int n,int m)
{
 if(m<n-m)
 {
  m=n-m;
 }
 long long ans=1;
 for(int i=m+1;i<=n;i++)
 {
  ans*=i;
 }
 for(int i=1;i<=n-m;i++)
 {
  ans/=i;
 }
 return ans;
}
int main ()
{
 int n,m;
 scanf("%d %d",&n,&m);
 printf("%lld",c(n,m));
 return 0;
}

汝佳老师提示

“对复杂的表达式进行化简有时不仅能减少计算量，还能减少甚至避免中间结果的溢出。”