Common Subsequence

原题及翻译

A subsequence of a given sequence is the given sequence with some elements (possible none) left out.
给定序列的子序列是给定序列，其中遗漏了一些元素（可能没有元素）。
Given a sequence X = < x1, x2, …, xm >
给定序列x=<x1，x2，…，xm>
another sequence Z = < z1, z2, …, zk >
另一个序列z=<z1，z2，…，zk>
is a subsequence of X if there exists a strictly increasing sequence < i1, i2, …, ik > of indices of X such that for all j = 1,2,…,k, x ij = zj.
是x的子序列，如果x的指数存在一个严格递增的序列<i1，i2，…，ik>，因此对于所有j=1，2，…，k，x ij=zj。
For example, Z = < a, b, f, c > is a subsequence of X = < a, b, c, f, b, c > with index sequence < 1, 2, 4, 6 >.
例如，z=<a，b，f，c>是索引序列<1，2，4，6>的x=<a，b，c，f，b，c>的子序列。
Given two sequences X and Y the problem is to find the length of the maximum-length common subsequence of X and Y.
给定两个序列x和y，问题是求x和y的最大长度公共子序列的长度。

Input

The program input is from the std input. Each data set in the input contains two strings representing the given sequences. The sequences are separated by any number of white spaces. The input data are correct.
程序输入来自标准输入。输入中的每个数据集包含两个表示给定序列的字符串。序列由任意数量的空格分隔。输入数据正确。

Output

For each set of data the program prints on the standard output the length of the maximum-length common subsequence from the beginning of a separate line.
对于每一组数据，程序在标准输出上打印从一个单独行开始的最大长度公共子序列的长度。

Sample Input

abcfbc abfcab
programming contest
abcd mnp

Sample Output

4
2
0

思路

输入两个串s1,s2,设MaxLen(i,j)表示:
s1的左边i个字符形成的子串，与s2左边的j个字符形成的子串的最长公共子序列的长度(i,j从0开始算）
MaxLen(i,j) 就是本题的“状态”
假定 len1 = strlen(s1),len2 = strlen(s2）那么题目就是要求 MaxLen(len1,len2）
显然：
MaxLen(n,0) = 0 ( n= 0…len1）
MaxLen(0,n) = 0 ( n= 0…len2）
递推公式：
if ( s1[i-1] == s2[j-1] ) //s1的最左边字符是s1[0]
MaxLen(i,j) = MaxLen(i-1,j-1) + 1;
else
MaxLen(i,j) = Max(MaxLen(i,j-1),MaxLen(i-1,j) );
时间复杂度O(mn) m,n是两个字串

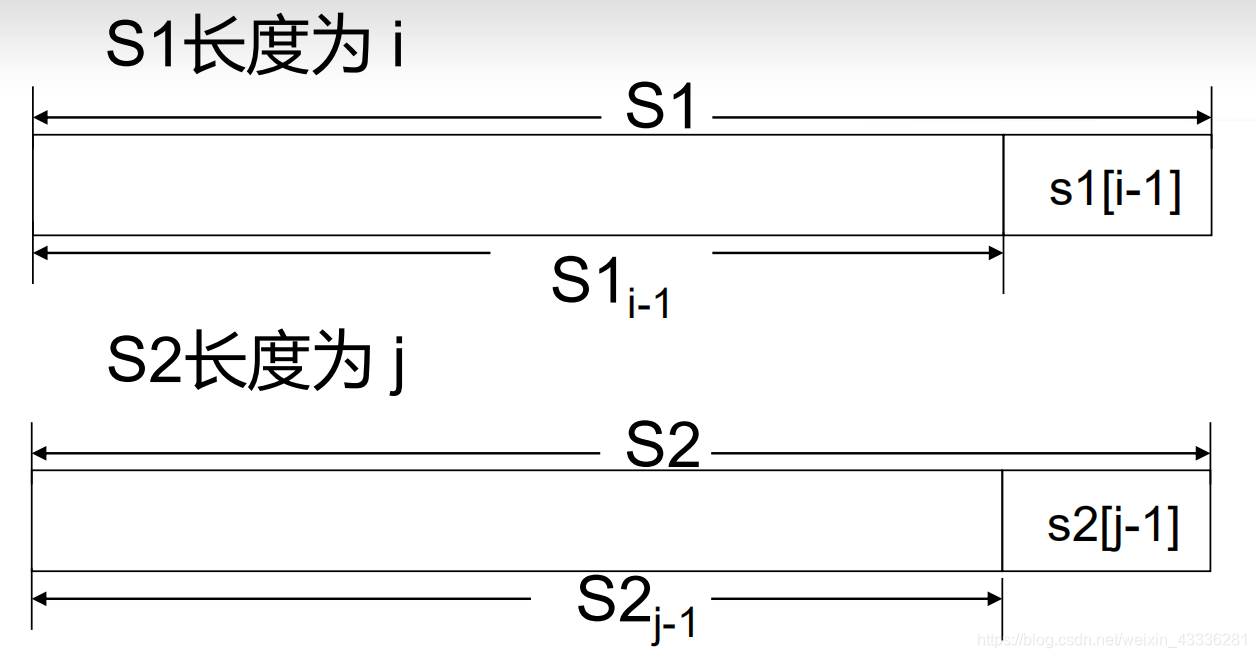
S1[i-1]!= s2[j-1]时，MaxLen(S1,S2)不会比MaxLen(S1,S2j-1) 和MaxLen(S1i-1,S2)两者之中任何一个小，也不会比两者都大。

代码分析

#include <iostream>
#include <cstring>
using namespace std;
char sz1[1000];
char sz2[1000];
int maxLen[1000][1000];
int main()
{
    while( cin >> sz1 >> sz2 )
	{
 	    int length1 = strlen( sz1);
 		int length2 = strlen( sz2);
 		int nTmp;
 		int i,j;
 		for( i = 0;i <= length1; i ++ )
 			 maxLen[i][0] = 0;
        for( j = 0;j <= length2; j ++ )
	  		 maxLen[0][j] = 0;
        for( i = 1;i <= length1;i ++ )
		{
	 	    for( j = 1; j <= length2; j ++ )
			 {
		  	     if( sz1[i-1] == sz2[j-1] )
				    maxLen[i][j] = maxLen[i-1][j-1] + 1;
 			     else
	 		        maxLen[i][j] = max(maxLen[i][j-1],maxLen[i-1][j]);
			 }
 		 }
  		 cout << maxLen[length1][length2] << endl;
		   }
	   return 0;
}