数据降维
1.特征选择
2.主成分分析
特征选择
特征选择原因
1.冗余:部分特征的相关度高,容易消耗计算性能。
2.噪声:部分特征对预测结果有影响。
1.特征选择是什么
特征选择就是单纯地从提取到的所有特征中选择部分特征作为训练集特征,特征在选择前和选择后可以改变值、也不改变值,但是选择后的特征维数肯定比选择前小。
主要方法(三大武器):
Filter(过滤式):VarianceThreshold
Embedded(嵌入式):正则化、决策树
Wrapper(包裹式)
Filter(过滤式):VarianceThreshold
sklearn特征选择API
sklearn.feature_selection.VarianceThreshold
VarianceThreshold语法
VarianceThreshold(threshold = 0.0)
删除所有低方差特征
Variance.fit_transform(X,y)
X:numpy array格式的数据[n_samples,n_features]
返回值:训练集差异低于threshold的特征将被删除。
默认值是保留所有非零方差特征,即删除所有样本
中具有相同值的特征。
流程:
1、初始化VarianceThreshold,指定阀值方差
2、调用fit_transform
演示:
from sklearn.feature_selection import VarianceThreshold
def var():
'''
特征选择-删除低方差的特征
:return:
'''
var=VarianceThreshold(threshold=0.0)
data=var.fit_transform([[0, 2, 0, 3], [0, 1, 4, 3], [0, 1, 1, 3]])
print(data)
return None
if __name__=='__main__':
var()

删除了方差为零的列。
主成分分析
sklearn降维API
sklearn. decomposition
PCA(主成分分析)
PCA是什么
本质:PCA是一种分析、简化数据集的技术。
目的:是数据维数压缩,尽可能降低原数据的维数(复杂度),损失少量信息。
作用:可以削减回归分析或者聚类分析中特征的数量。
特征数量达到上百的时候,考虑数据我的简化,特征也会改变,特征数量也会减少。
高维度数据容易出现的问题:特征之间通常是相关的。
数据:
(-1,-2)
(-1, 0)
( 0, 0)
( 2, 1)
( 0, 1)
要求:将这个二维的数据简化成一维?
 通过公式计算
通过公式计算

矩阵运算得出P为
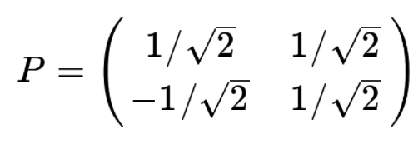
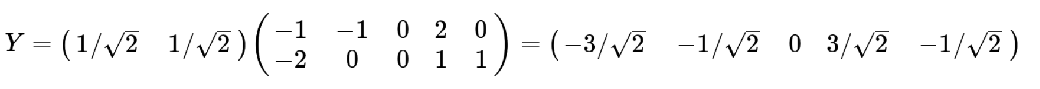
PCA语法
PCA(n_components=None)
将数据分解为较低维数空间
PCA.fit_transform(X)
X:numpy array格式的数据[n_samples,n_features]
返回值:转换后指定维度的array
流程:
1、初始化PCA,指定减少后的维度
2、调用fit_transform
演示:
from sklearn.decomposition import PCA
def pca():
'''
主成分分析进行数据降维
:return: None
'''
pca=PCA(n_components=0.9)
data=pca.fit_transform([[2,8,4,5],[6,3,0,8],[5,4,9,1]])
print(data)
return None
if __name__=="__main__":
pca()
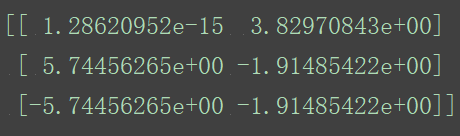
数据由三个特征降为两个特征。