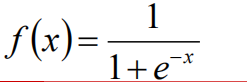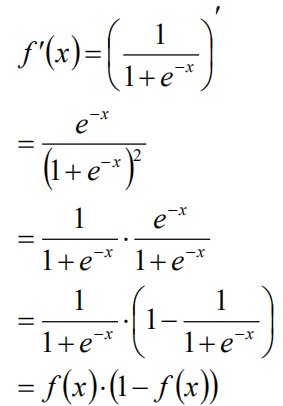机器学习与数学分析
机器学习概述
什么是机器学习
1.对于某给定的任务T，在合理的性能度量方案P的前提下，某计算机程序可以自主学习任务T和经验E；随着提供合适、优质、大量的经验E，该程序对于任务T的性能逐步提高。
2.这里最重要的是机器学习的对象：
（1）、任务Task.T，一个或者多个。
（2）、经验Experience.E。
（3）、性能Performance.P。
3.随着任务的不断执行，经验的累积会带来计算机性能的提升。
简易表述
机器学习是人工智能的一个分支。
我们使用计算机设计一个系统，使它能够根据提供的训练数据按照一定的方式来学习。
随着训练次数的增加，该系统可以在性能上不断学习和改进。
通过参数优化的学习模型，能够用于预测相关问题的输出。
思考：如何设计无人驾驶机动车？
无人驾驶汽车
汽车的无人驾驶模块已经成熟：全自动公共交通工具已经出现在了世界上的多个城市。
问题：如何设计自动驾驶系统？
人类的学习
1.如何从完全“无知”到掌握知识
2.有监督学习
3.无监督学习
4.增强学习
机器学习的内涵与外延
机器学习可以解决什么
给定数据的预测问题：
1.数据清洗/特征选择
2.确定算法模型/参数优化
3.结果预测
……
不能解决什么
大数据存储/并行计算
做一个机器人
……
机器学习的一般流程
数据收集——>数据清洗——>特征工程——>数据建模
机器学习方法
different assumption on data
different scalability profiles at training time
different latencies at prediction time
different model sizes （embedability in mobile devices）
思考：机器如何发现新词
频数：Count（X）
凝固程度
X=A.B
P（A）P（B） VS P（X）
自由程度
aXb
信息熵H（a）、H（b）
凝固程度和自由程度缺一不可，还需要调参。
问题：给定某长文本，如何利用上述参数设计可行算法？
机器学习的角度看数学
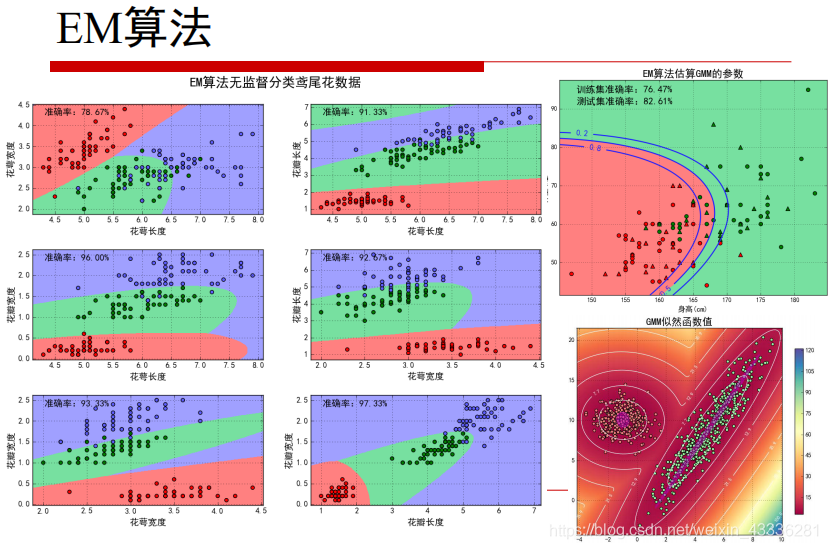
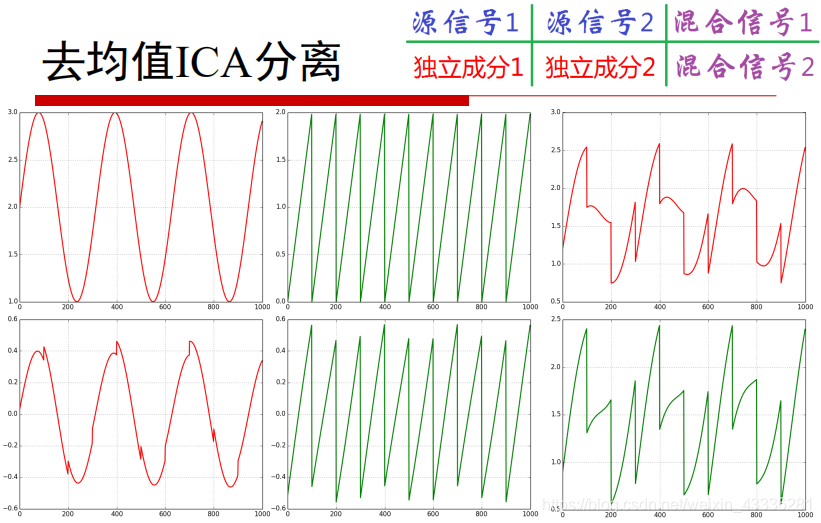
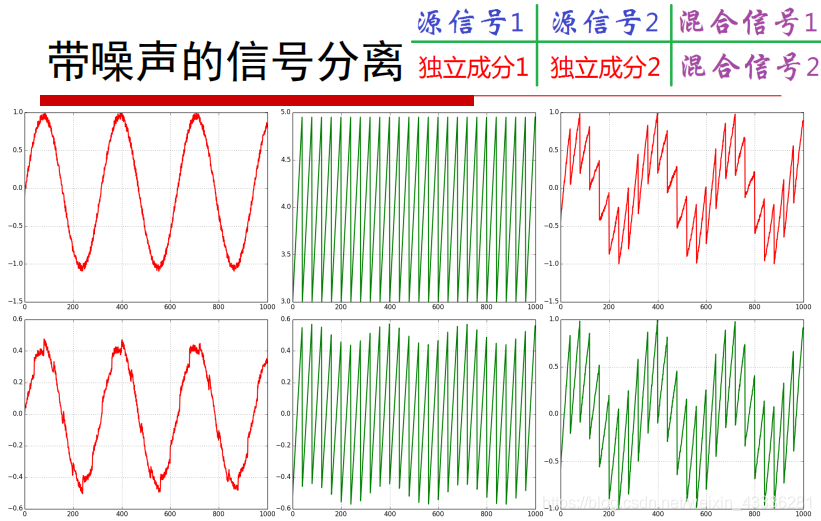
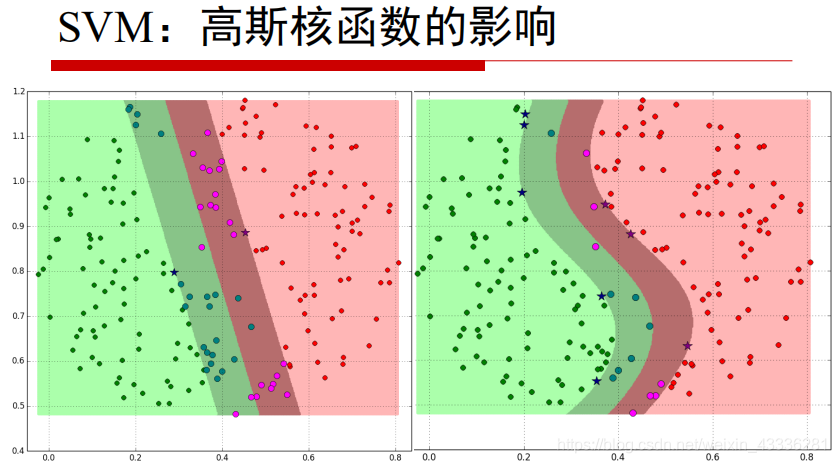
理解HMM框架
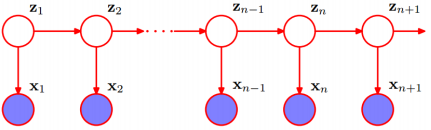
概率计算问题
1.给定模型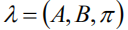
和观测序列O={o1,o2,……ot}，计算模型λ下观测序列O出现的概率P（O|λ）
2.前向-后向算法——动态规划。
学习问题
1.已知观测序列O={o1,o2,……ot}，估计模型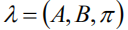的参数，使得在该模型下观测序列P（O|λ）最大。
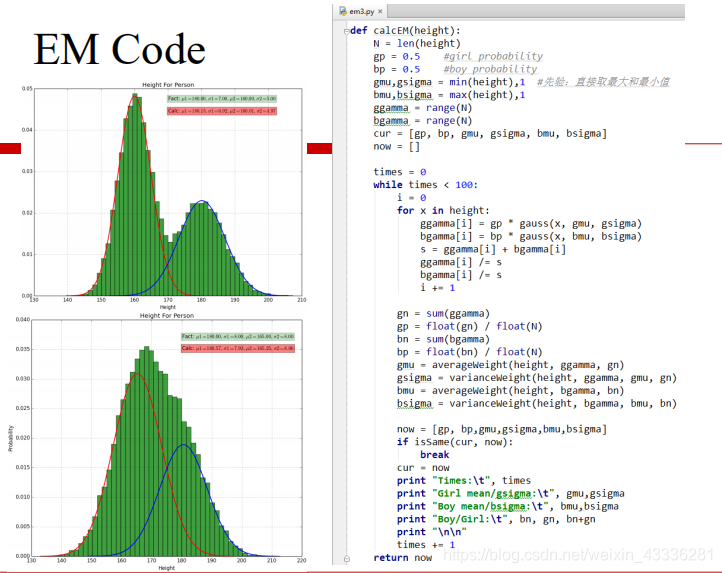
2.最大似然估计（给定状态序列），Baum-Welch算法（状态序列未知）——EM算法。
预测问题
1.即解码问题：已知模型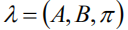和观测序列O={o1,o2,……ot}，求对给定观测序列条件概率P（O|λ）最大的状态序列I。
2.Viterbi算法——动态规划。
数学分析
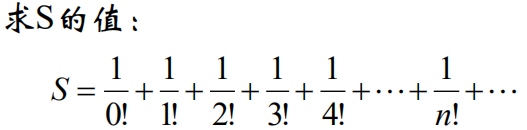
问题分析
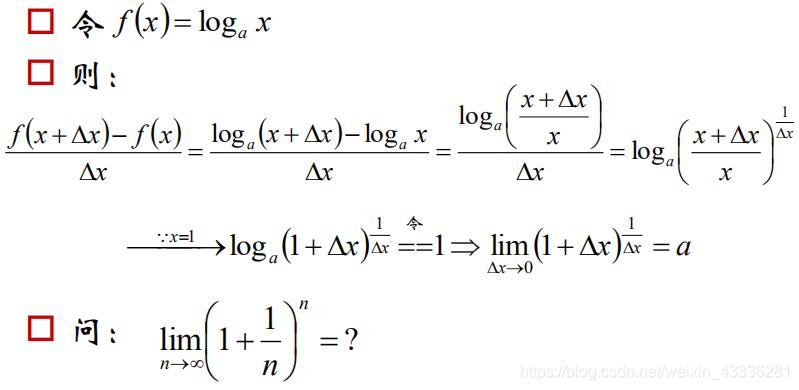
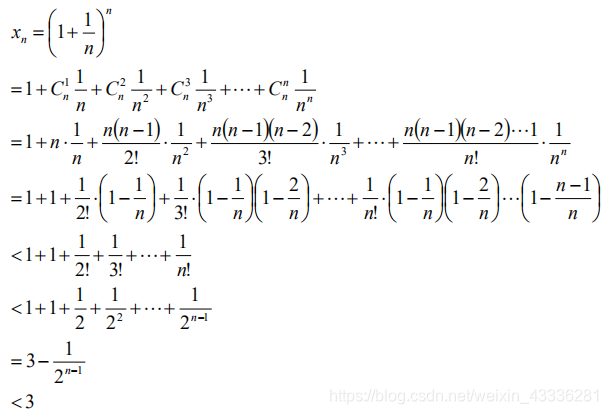
导数与梯度
导数
1.简单的说，导数就是曲线的斜率，是曲线变化快慢的反应。
2.二阶导数是斜率变化快慢的反应，表征曲线的凸凹性。二阶导数连续的曲线，往往称之为“光顺”的。
3.根据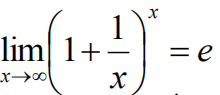
可以得到函数f(x)=ln x的导数，进一步根据换底公式、反函数求导等，得到其它初等函数的导数。
常用函数的导数
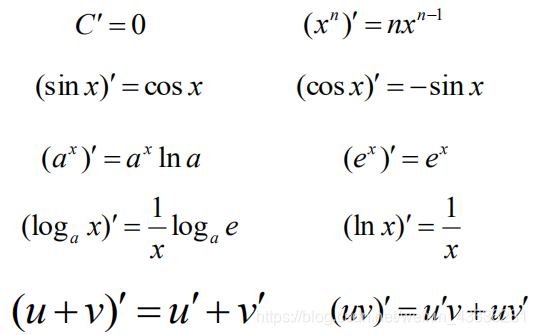
方向导数
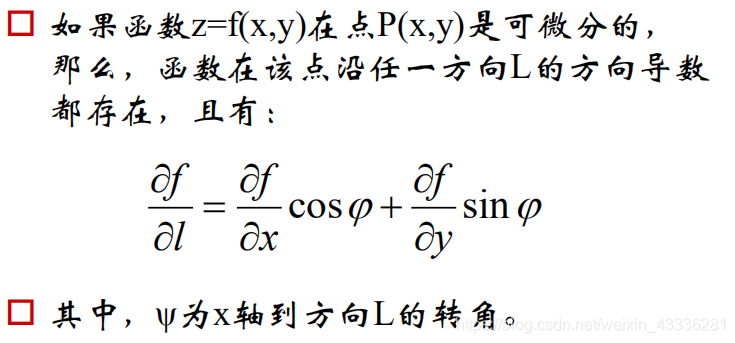
梯度
积分应用
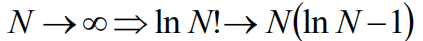
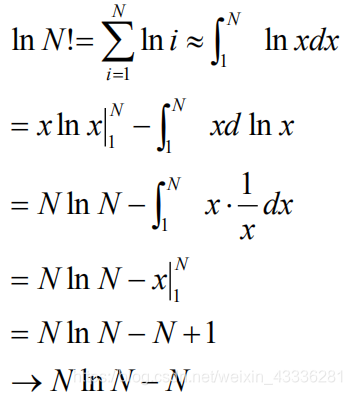
Taylor展式的应用
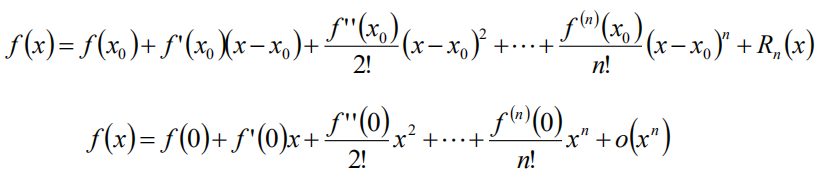
Taylor公式的应用
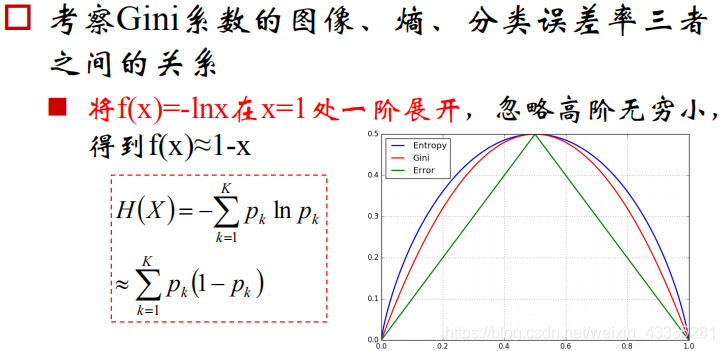
概率论基础
概率论
古典概型
解：
概率公式
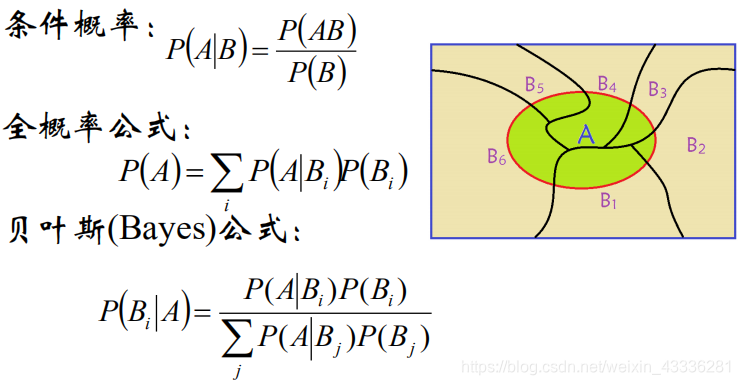
频率学派与贝叶斯学派
贝叶斯公式
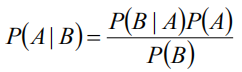
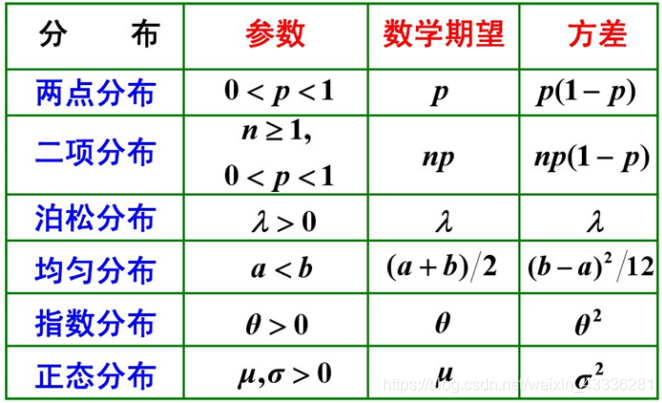
常见概率分布
两点分布
二项分布 Bernoulli distribution
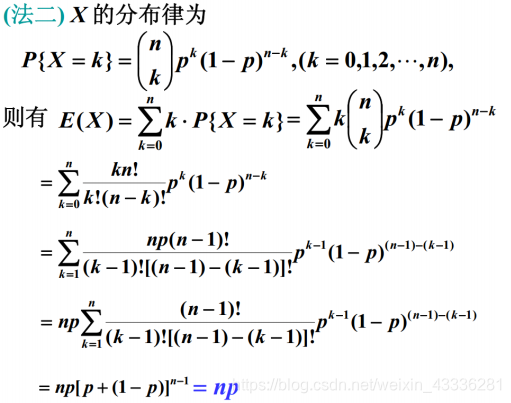
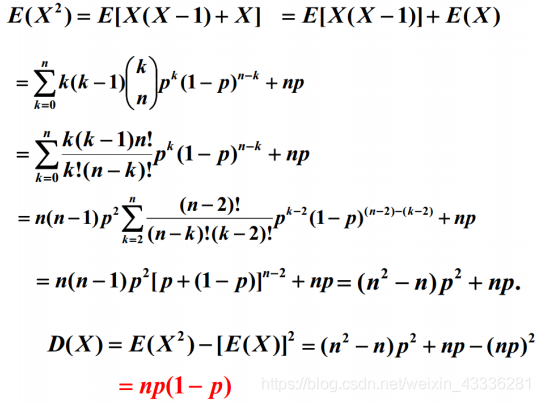
考察Taylor展式
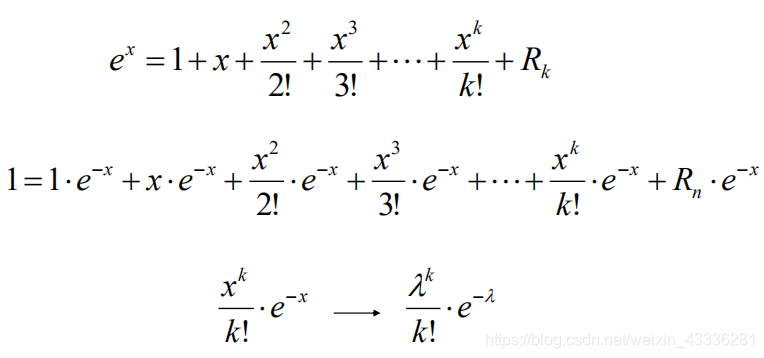
泊松分布
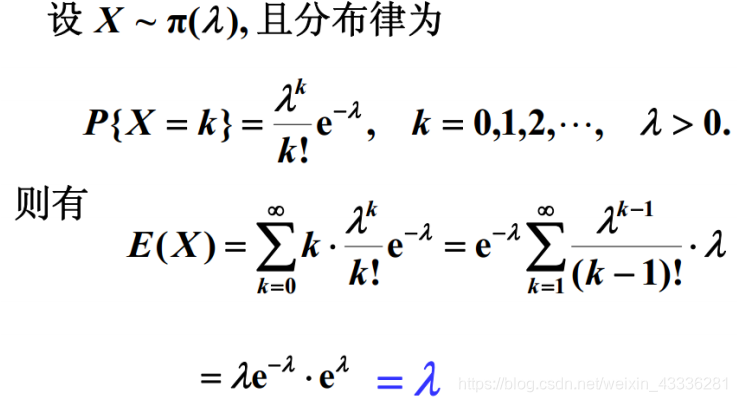
均匀分布
指数分布
指数分布的无记忆性
正态分布
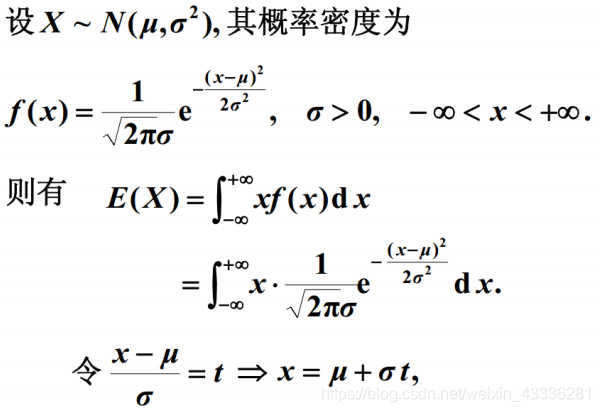
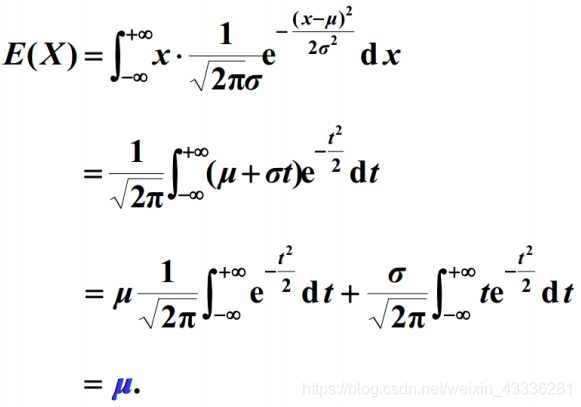
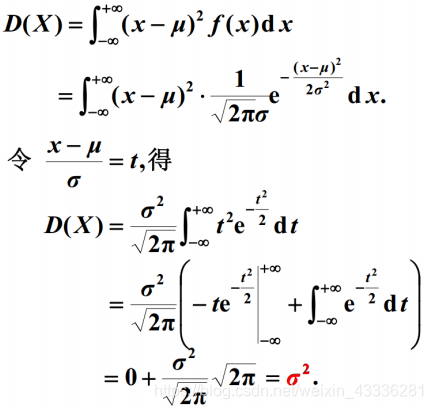
二元正态分布
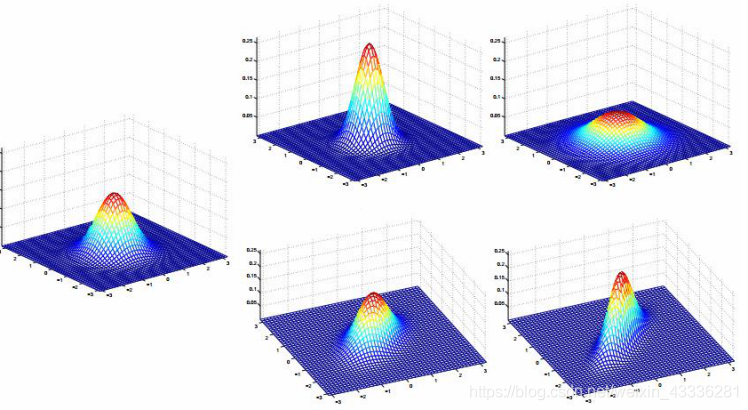
总结
Sigmoid/Logistic函数的引入
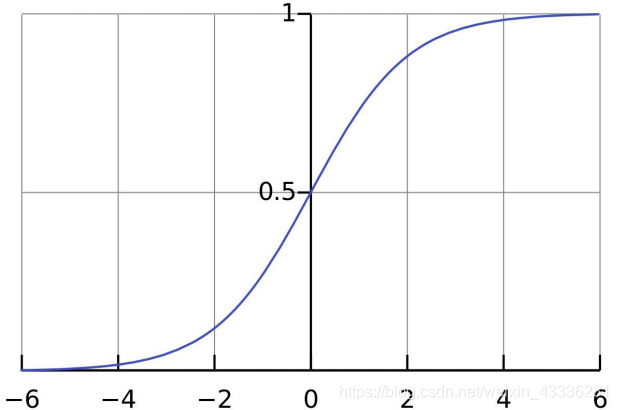
Sigmoid函数的导数
