基本思想
每一趟从待排序的数据元素中选出最小(或最大)的一个元素,顺序放在待排序的数列最前,直到全部待排序的数据元素排完。
具体步骤
1.读入数据存放在a数组中。
2.在a[1]~a[n]中选择值最小的元素,与第1位置元素交换,则把最小值元素放入a[1]中。
3.在a[2]~a[n]中选择值最小的元素,与第2位置元素交换,则把最小值元素放入a[2]中,……
4.直到n-1个元素与第n个元素比较排序为止。
实现方法
程序用两层循环完成算法,外层循环i控制当前序列最小值存放的数组位置,内层循环j控制从i+1到n序列中选择最小的元素所在位置k。
程序代码
#include <iostream>
using namespace std;
int main ()
{
int n,temp,array[1000];
cin>>n;
array[0]=n;
for (int i = 1; i <= n ; ++i)
{
cin>>array[i];
}
for (int i = 1; i <= n; ++i)
{
for (int j = i+1; j <= n; ++j)
{
if(array[j]<array[i])
{
temp=array[i];
array[i]=array[j];
array[j]=temp;
}
}
}
for (int k = 1; k <= n; ++k)
{
cout<<array[k]<<' ';
}
return 0;
}
测试
#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;
int main ()
{
int n,temp,array[1000];
// cin>>n;
// array[0]=n;
// for (int i = 1; i <= n ; ++i)
// {
// cin>>array[i];
// }
n=1000;
srand(time(NULL));
for (int i=1;i<=n;i++)
array[i]=rand()%10000;
for (int i = 1; i <= n; ++i)
{
for (int j = i+1; j <= n; ++j)
{
if(array[j]<array[i])
{
temp=array[i];
array[i]=array[j];
array[j]=temp;
}
}
}
for (int k = 1; k <= n; ++k)
{
cout<<array[k]<<' ';
}
cout<<endl;
printf("Time used = %.7lf",(double)clock()/CLOCKS_PER_SEC);
return 0;
}
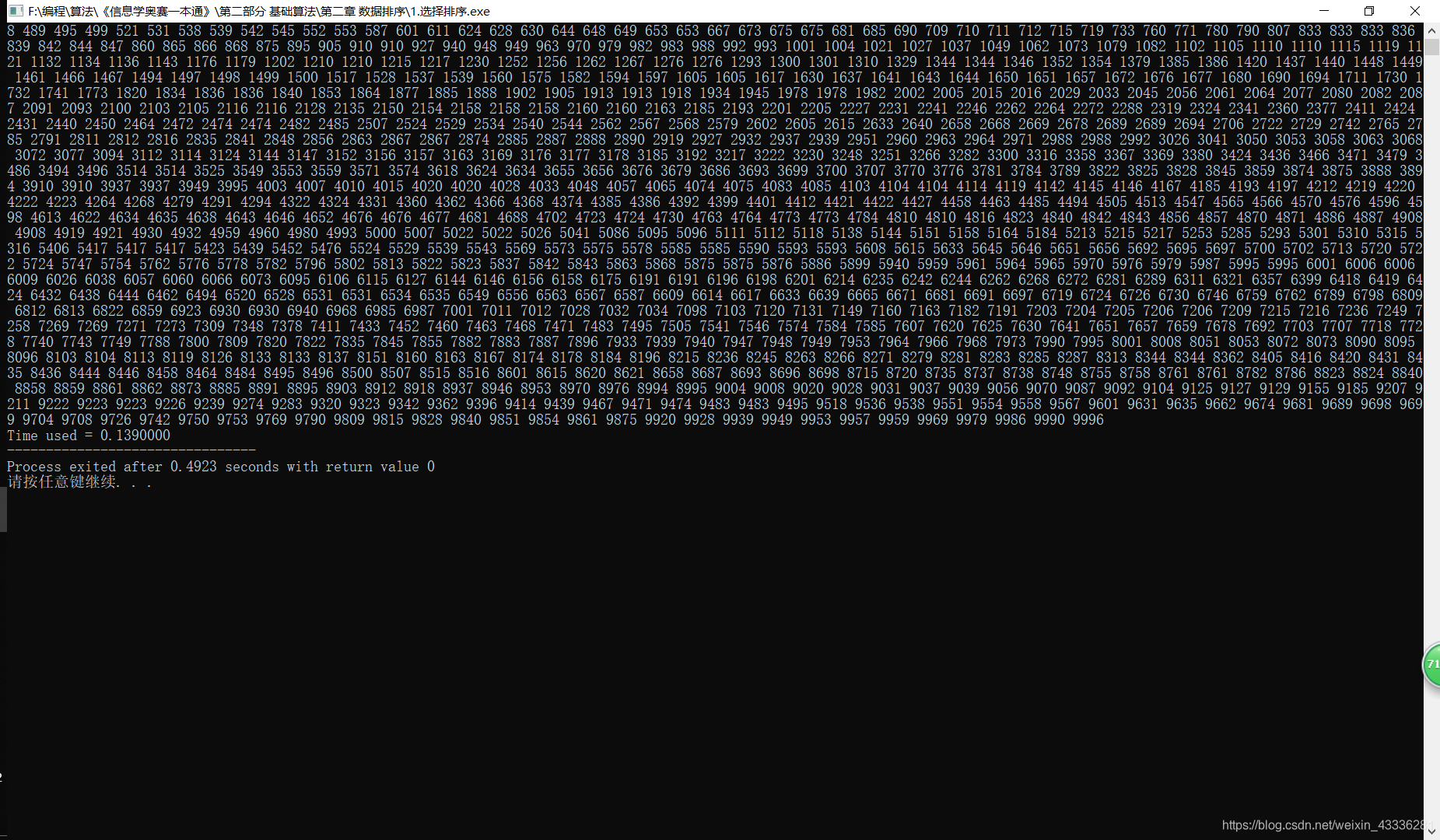
算法分析
时间复杂度
选择排序的交换操作介于 0 和 (n - 1) 次之间。
选择排序的比较操作为 (n-1)+(n-2)+……+3+2+1+0=n (n - 1) / 2 次之间。
选择排序的赋值操作介于 0 和 3 (n - 1) 次之间。
比较次数O(n2),比较次数与关键字的初始状态无关,
总的比较次数N=(n-1)+(n-2)+…+1=n*(n-1)/2。
交换次数O(n),最好情况是,已经有序,交换0次;最坏情况交换n-1次,逆序交换n/2次。
交换次数比冒泡排序少多了,由于交换所需CPU时间比比较所需的CPU时间多,n值较小时,选择排序比冒泡排序快。
稳定性
选择排序是给每个位置选择当前元素最小的,比如给第一个位置选择最小的,在剩余元素里面给第二个元素选择第二小的,依次类推,直到第n-1个元素,第n个元素不用选择了,因为只剩下它一个最大的元素了。
那么,在一趟选择,如果一个元素比当前元素小,而该小的元素又出现在一个和当前元素相等的元素后面,那么交换后稳定性就被破坏了。
比较拗口,举个例子,序列5 8 5 2 9,我们知道第一遍选择第1个元素5会和2交换,那么原序列中两个5的相对前后顺序就被破坏了,所以选择排序是一个不稳定的排序算法。