排序算法 —— 冒泡排序

基本思想

n个元素，从第1个开始，依次比较相邻的两个是否逆序对（大在前，小在后），若逆序就交换两个元素，即第1个和第2个比，若逆序就交换两个元素，接着第2个和第3个比，若逆序就交换两个元素，接着第3个和第4个比，若逆序就交换两个元素，……，直到n-1和n比较，经过一轮比较后，则把最大的元素排到最后，即将最大的元素像冒泡一样逐步冒到相应的位置。原来n个元素的排序问题，转换为n-1个元素的排序问题。第二轮从第1个开始，依次比较相邻的两个元素是否逆序对，若逆序就交换两个元素，知道n-2和n-1比较。如此，进行n-1轮后，队列为有序的队列。

具体步骤

1.读入数据存放在a数组中。

2.比较相邻的前后两个数据，如果前面数据大于后面的数据，就将两个数据交换。

3.对数组的第0个数据到n-1个数据进行一次遍历后，最大的一个数据就“冒”到数组的第n-1个位置。

4.n=n-1，如果n不为0就重复前面两步，否则排序完成。

实现方法

程序用两层循环完成算法，外层循环i控制每轮要进行多少次的比较，第1轮比较n-1次，第2轮比较n-2次，……，最后一次比较1次。内层循环j控制每轮i次比较相邻两个元素是否逆序，若逆序就交换这两个元素。

程序代码

#include <iostream>
using namespace std;
int main ()
{
	int n,temp,array[1000];
	cin>>n;
	array[0]=n;
	for(int i=1;i<=n;i++)
	{
		cin>>array[i];
	}
	for(int i=1;i<n;i++)
	{
		bool ok=true;
		for(int j=1;j<=n-i;j++)
		{
			if(array[j]>array[j+1])
			{
				ok=false;
				temp=array[j+1];
				array[j+1]=array[j];
				array[j]=temp;
			}
		}
		if(ok) break;
	}
	for(int i=1;i<=n;i++)
	{
		cout<<array[i]<<' ';
	}
	return 0;
}

测试

#include <iostream>
#include <cstdio>
#include <cstdlib>
#include <ctime>
using namespace std;
int main ()
{
	int n,temp,array[1000];
//	cin>>n;
//	array[0]=n;
//	for(int i=1;i<=n;i++)
//	{
//		cin>>array[i];
//	}

	n=1000;
	srand(time(NULL));
    for (int i=1;i<=n;i++)
    array[i]=rand()%10000;
    
	for(int i=1;i<n;i++)
	{
		bool ok=true;
		for(int j=1;j<=n-i;j++)
		{
			if(array[j]>array[j+1])
			{
				ok=false;
				temp=array[j+1];
				array[j+1]=array[j];
				array[j]=temp;
			}
		}
		if(ok) break;
	}
	for(int i=1;i<=n;i++)
	{
		cout<<array[i]<<' ';
	}
	
	cout<<endl;
    printf("Time used = %.7lf",(double)clock()/CLOCKS_PER_SEC);
	return 0;
}

算法分析

时间复杂度

若文件的初始状态是正序的，一趟扫描即可完成排序。

所需的关键字比较次数C和记录移动次数M均达到最小值：C_min=n-1，M_min=0。

所以，冒泡排序最好的时间复杂度为O（n）。

若初始文件是反序的，需要进行n-1趟排序。

每趟排序要进行n-i次关键字的比较(1≤i≤n-1)，且每次比较都必须移动记录三次来达到交换记录位置。在这种情况下，比较和移动次数均达到最大值：

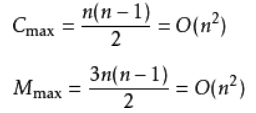
冒泡排序的最坏时间复杂度为O（n²）。
综上，因此冒泡排序总的平均时间复杂度为O（n²）。

算法稳定性

冒泡排序就是把小的元素往前调或者把大的元素往后调。

比较是相邻的两个元素比较，交换也发生在这两个元素之间。

所以，如果两个元素相等，是不会再交换的；如果两个相等的元素没有相邻，那么即使通过前面的两两交换把两个相邻起来，这时候也不会交换，所以相同元素的前后顺序并没有改变，所以冒泡排序是一种稳定排序算法。