在所有的递推关系中,斐波那契数列应该是最为熟悉的。
在最基础的程序设计语言Logo语言中,就有很多这类的题目。
而在较为复杂的Basic、Pascal、C语言中,斐波那契数列类的题目因为解法的相对容易一些,逐渐退出了竞赛的舞台。
可是这不等于说斐波那契数列没有研究价值。
Fabonacci数列常出现在比较简单的组合计数问题中。
在优化法中,Fabonacci数列的用处也得到了较好的体现。
兔子数列
在这本书中,斐波那契提出了一个问题:
在第一个月有一对刚出生的小兔子,在第二个月小兔子变成大兔子并开始怀孕,第三个月大兔子会生下一对小兔子,并且以后每个月都会生下一对小兔子。 如果每对兔子都经历这样的出生、成熟、生育的过程,并且兔子永远不死,那么兔子的总数是如何变化的?
我们不妨先来看个图:

第一个月只有一对兔宝宝,1对兔子。
第二个月兔宝宝变成大兔子,1对兔子。
第三个月大兔子生了一对兔宝宝,一大一小2对兔子。
第四个月大兔子继续生一对兔宝宝,小兔子变成大兔子。两大一小3对兔子。
….
我们把这个数列列表

我们发现会发现以下几个规律:
前一个月的大兔子对数就是下一个月的小兔子对数。
前一个月的大兔子和小兔子对数的和就是下个月大兔子的对数。
按照这个表格,我们会发现无论是小兔子对数、大兔子对数还是总对数,除了最初几个数字不一样之外,后面都是按照1、1、2、3、5、8、13…变化的,这个数列就称为兔子数列或者斐波那契数列。
兔子数列最大的特点就是前两项之和等于后一项,比如1+1=2、1+2=3、2+3=5、3+5=8、5+8=13…
我们用an表示一个数列的第n项,那么斐波那契数列的规律就是
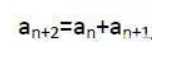
这种式子称为递推式,也就是说可以从前面一项或几项,计算出后面一项的式子。再结合前两项a1=a2=1,就可以得到后面任意一项了。
神奇的数列
也许许多人觉得,斐波那契数列不过是浩如烟海的数学海洋中的一滴水。但是实际上,从这个数列被提出的那一天起,几百年来人们在许多领域都发现了它的影子。
在数学上,许多求“方法数”的问题,答案都是斐波那契数列。例如:如果我们要上一个N级台阶的楼梯,每次只能走1格或者2格,那么一共有多少种走法呢?
如果只有一级台阶,显然只有1种走法。
如果有两级台阶,显然可以走一步,也可以走两步,因此有2种走法。
如果有三级台阶,就有如图所示的3种走法。
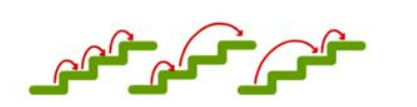
1、2、3这三个数字都是斐波那契数。那么,如果有更多台阶怎么办呢?这就需要递推式了。
由于一步最多走连两个台阶,因此要到达第N级台阶,有两种方案:
走到第N-1级台阶上,然后走1级台阶跨到最上方;
走到第N-2级台阶上,然后一步走两级台阶跨到最上方。
注意,从第N-2级台阶走1级到N-1级台阶这种情况已经在第一种情况中计算过了。
用a(N-1)和a(N-2)分别表示走到第N-1级和第N-2级台阶的方法数,那么走到第N级台阶的方法数就是:
aN= a(N-1)+ a(N-2)
显然,这就是斐波那契数列的递推公式,因此走台阶问题的解刚好是斐波那契数列。
生活中最典型的斐波那契数列应用是在植物学中。

大树在生长的过程中会长出分枝,如果我们从下到上数分枝个数,就会发现依次是1、1、2、3、5、8、13…等等,刚好是斐波那契数列。
有科学家对这种现象的解释是与兔子繁殖后代相同:每过一段时间老树枝都会萌发新芽,而新芽成长为成熟的树枝后也会每隔一段时间萌发一次新芽。
另一个神奇的例子就是向日葵等植物。

如果我们仔细观察,就会发现向日葵盘内的种子形成两组螺旋线,一组是顺时针的,另一组是逆时针的。
而这两组螺旋线的条数刚好是两个相邻的斐波那契数,小向日葵是34和55,大向日葵是144和233。
松果种子、菜花表面也有类似的规律。

有科学家认为:这种排列可以使得种子的堆积最密集,最有利于植物繁衍后代。
八百年来,人们在各个领域都发现了斐波那契数列。
尤其是十九世纪开始,人们发现了斐波那契数列在计算机、物理、化学等领域的应用,这个古老的数列焕发了新的青春。
1963年,斐波那契协会成立,并出版了《斐波那契季刊》用以刊登与斐波那契数列相关的研究成果。
代码实现
基本循环算法
# include <iostream>
# include <cstdio>
using namespace std;
int main(){
int a=0,b=1,c=1,n;
cin>>n;//输入n
for(int i=3;i<=n;i++){
a=b;
b=c;
c=a+b;
}
cout<<c; //输出最终结果
return 0;
}
递归算法实现
# include <iostream>
# include <cstdio>
using namespace std;
int f(int n){
if(n==0) return 0;
if(n==1) return 1;
if(n>=2){
return f(n-1)+f(n-2);
}
}
int main(){
int n;
cin>>n;
printf("%d",f(n));
return 0;
}
递归算法优化(记忆化搜索)
# include <iostream>
# include <cstdio>
# define MAX (101)
using namespace std;
int a[MAX];
int f(int n){
if(a[n]!=-1) return a[n];
else{
a[n]=f(n-1)+f(n-2);
return a[n];
}
}
int main(){
int n;
cin>>n;
for(int i=0;i<=MAX-1;i++){ //初始化
a[i]=-1;
}
a[0]=0;a[1]=1;
printf("%d",f(n));
return 0;
}
高精度计算
#include<iostream>
#include<cstring>
using namespace std;
char sum[1200];
int s=0,m=0,n;
int main()
{
cin>>n;
string s1,s2;
int a[1200],b[1200],he,i;
s1="0";s2="1";
for(m=2;m<n;m++)
{
memset(a,0,sizeof(a));
memset(b,0,sizeof(b));
a[0]=s1.length();
for(i=1;i<=a[0];i++)
a[i]=s1[a[0]-i]-'0';
b[0]=s2.length();
for(i=1;i<=b[0];i++)
b[i]=s2[b[0]-i]-'0';
he=(a[0]>b[0]?a[0]:b[0]);
for(i=1;i<=he;i++)
{
a[i]+=b[i];
a[i+1]+=a[i]/10;
a[i]%=10;
}
he++;
while((a[he]==0)&&(he>1))he--;
for(i=he,s=0;i>=1;i--,s++)
sum[s]=a[i]+'0';
s1=s2;
s2=sum;
}
cout<<s2<<endl;
return 0;
}