算法效率的度量方法
事后统计方法
这种方法主要是通过设计好的测试程序和数据,利用计算机计时器对不同算法编制的程序的运行时间进行比较,从而确定算法效率的高低。
但这种方法显然是有很大缺陷的:
必须依据算法事先编制好测试程序,通常需要花费大量时间和精力;
不同测试环境差别不是一般的大!
事前分析估算方法
在计算机程序编写前,依据统计方法对算法进行估算。
- 算法采用的策略,方案
- 编译产生的代码质量
- 问题的输入规模
- 机器执行指令的速度
由此可见,抛开这些与计算机硬件、软件有关的因素,一个程序的运行时间依赖于算法的好坏和问题的输入规模。(所谓的问题输入规模是指输入量的多少)
不关心编写程序所用的语言是什么,也不关心这些程序将跑在什么样的计算机上,只关心它所实现的算法。
这样,不计那些循环索引的递增和循环终止条件、变量声明、打印结果等操作。
最终,在分析程序的运行时间时,最重要的是把程序看成是独立于程序设计语言的算法或一系列步骤。
在分析一个算法的运行时间时,重要的是把基本操作的数量和输入模式关联起来。
函数的渐近增长
给定两个函数f(n)和g(n),如果存在一个整数N,使得对于所有的n>N,f(n)总是比g(n)大,那么,我们说f(n)的增长渐近快于g(n)。
最高次项的指数大的,函数随着n的增长,结果也会变得增长特别快。
判断一个算法的效率时,函数中的常数和其他次要项常常可以忽略,而更应该关注主项(最高项)的阶数。
算法时间复杂度
算法时间复杂度的定义:在进行算法分析时,语句总的执行次数T(n)是关于问题规模n的函数,进而分析T(n)随n的变化情况并确定T(n)的数量级。
算法的时间复杂度,也就是算法的时间量度,记作:T(n)= O(f(n))。它表示随问题规模n的增大,算法执行时间的增长率和f(n)的增长率相同,称作算法的渐近时间复杂度,简称为时间复杂度。其中f(n)是问题规模n的某个函数。
这样用大写O()来体现算法时间复杂度的记法,我们称之为大O记法。
一般情况下,随着输入规模n的增大,T(n)增长最慢的算法为最优算法。
如何推导大O阶?
1.用常数1取代运行时间中的所有加法常数。
2.在修改后的运行次数函数中,只保留最高阶项。
3.如果最高阶项存在且不是1,则去除与这个项相乘的常数。
4.得到的最后结果就是大O阶。
常见的时间复杂度
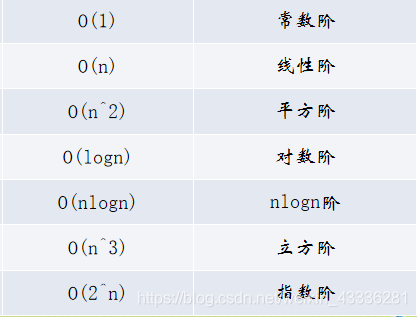
常用的时间复杂度所耗费的时间从小到大依次是:
O(1) < O(logn) < (n) < O(nlogn) < O(n ^ 2) < O(n ^ 3) < O(2 ^ n) < O(n!) < O(n ^ n)
空间复杂度
算法的空间复杂度通过计算算法所需的存储空间实现,算法的空间复杂度的计算公式记作:S(n)=O(f(n)),其中,n为问题的规模,f(n)为语句关于n所占存储空间的函数。
通常,我们都是用“时间复杂度”来指运行时间的需求,是用“空间复杂度”指空间需求。
当直接要让我们求“复杂度”时,通常指的是时间复杂度。