Search trees are data structures that support dynamic set operations including insert, search, delete and so on. Thus a search tree can be used both as a dictionary and as a priority queue.
Binary search tree is one of fundamental search trees. The keys in a binary search tree are always stored in such a way as to satisfy the following binary search tree property:
Let x be a node in a binary search tree. If y is a node in the left subtree of x, then y.key≤x.key. If y is a node in the right subtree of x, then x.key≤y.key.
The following figure shows an example of the binary search tree.
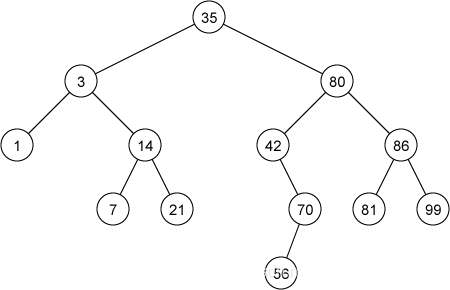
For example, keys of nodes which belong to the left sub-tree of the node containing 80 are less than or equal to 80, and keys of nodes which belong to the right sub-tree are more than or equal to 80. The binary search tree property allows us to print out all the keys in the tree in sorted order by an inorder tree walk.
A binary search tree should be implemented in such a way that the binary search tree property continues to hold after modifications by insertions and deletions. A binary search tree can be represented by a linked data structure in which each node is an object. In addition to a key field and satellite data, each node contains fields left, right, and p that point to the nodes corresponding to its left child, its right child, and its parent, respectively.
To insert a new value v into a binary search tree T, we can use the procedure insert as shown in the following pseudo code. The insert procedure is passed a node z for which z.key=v, z.left=NIL, and z.right=NIL. The procedure modifies T and some of the fields of z in such a way that z is inserted into an appropriate position in the tree.
1 insert(T, z)
2 y = NIL // parent of x
3 x = ‘the root of T’
4 while x ≠ NIL
5 y = x // set the parent
6 if z.key < x.key
7 x = x.left // move to the left child
8 else
9 x = x.right // move to the right child
10 z.p = y
11
12 if y == NIL // T is empty
13 ‘the root of T’ = z
14 else if z.key < y.key
15 y.left = z // z is the left child of y
16 else
17 y.right = z // z is the right child of y
Write a program which performs the following operations to a binary search tree T.
insert k: Insert a node containing k as key into T.
print: Print the keys of the binary search tree by inorder tree walk and preorder tree walk respectively.
You should use the above pseudo code to implement the insert operation. T is empty at the initial state.
Input
In the first line, the number of operations m is given. In the following m lines, operations represented by insert k or print are given.
Output
For each print operation, print a list of keys obtained by inorder tree walk and preorder tree walk in a line respectively. Put a space character before each key.
Constraints
The number of operations ≤500,000
The number of print operations ≤10.
−2,000,000,000≤key≤2,000,000,000
The height of the binary tree does not exceed 100 if you employ the above pseudo code.
The keys in the binary search tree are all different.
Sample Input 1
8
insert 30
insert 88
insert 12
insert 1
insert 20
insert 17
insert 25
print
Sample Output 1
1 12 17 20 25 30 88
30 12 1 20 17 25 88
Reference
Introduction to Algorithms, Thomas H. Cormen, Charles E. Leiserson, Ronald L. Rivest, and Clifford Stein. The MIT Press.
Code
/*
^....0
^ .1 ^1^
.. 01
1.^ 1.0
^ 1 ^ ^0.1
1 ^ ^..^
0. ^ 0^
.0 1 .^
.1 ^0 .........001^
.1 1. .111100....01^
00 11^ ^1. .1^
1.^ ^0 0^
.^ ^0..1
.1 1..^
1 .0 ^ ^
00. ^^0.^
^ 0 ^^110.^
0 0 ^ ^^^10.01
^^ 10 1 1 ^^^1110.1
01 10 1.1 ^^^1111110
010 01 ^^ ^^^1111^1.^ ^^^
10 10^ 0^ 1 ^^111^^^0.1^ 1....^
11 0 ^^11^^^ 0.. ....1^ ^ ^
1. 0^ ^11^^^ ^ 1 111^ ^ 0.
10 00 11 ^^^^^ 1 0 1.
0^ ^0 ^0 ^^^^ 0 0.
0^ 1.0 .^ ^^^^ 1 1 .0
^.^ ^^ 0^ ^1 ^^^^ 0. ^.1
1 ^ 11 1. ^^^ ^ ^ ..^
^..^ ^1 ^.^ ^^^ .0 ^.0
0..^ ^0 01 ^^^ .. 0..^
1 .. .1 ^.^ ^^^ 1 ^ ^0001
^ 1. 00 0. ^^^ ^.0 ^.1
. 0^. ^.^ ^.^ ^^^ ..0.0
1 .^^. .^ 1001 ^^ ^^^ . 1^
. ^ ^. 11 0. 1 ^ ^^ 0.
0 ^. 0 ^0 1 ^^^ 0.
0.^ 1. 0^ 0 .1 ^^^ ..
.1 1. 00 . .1 ^^^ ..
1 1. ^. 0 .^ ^^ ..
0. 1. .^ . 0 .
.1 1. 01 . . ^ 0
^.^ 00 ^0 1. ^ 1 1
.0 00 . ^^^^^^ .
.^ 00 01 ..
1. 00 10 1 ^
^.1 00 ^. ^^^ .1
.. 00 .1 1..01 ..
1.1 00 1. ..^ 10
^ 1^ 00 ^.1 0 1 1
.1 00 00 ^ 1 ^
. 00 ^.^ 10^ ^^
1.1 00 00 10^
..^ 1. ^. 1.
0 1 ^. 00 00 .^
^ ^. ^ 1 00 ^0000^ ^ 01
1 0 ^. 00.0^ ^00000 1.00.1 11
. 1 0 1^^0.01 ^^^ 01
.^ ^ 1 1^^ ^.^
1 1 0.
.. 1 ^
1 1
^ ^ .0
1 ^ 1
.. 1.1 ^0.0
^ 0 1..01^^100000..0^
1 1 ^ 1 ^^1111^ ^^
0 ^ ^ 1 1000^
.1 ^.^ . 00
.. 1.1 0. 0
1. . 1. .^
1. 1 1. ^0
^ . ^.1 00 01
^.0 001. .^
*/
// Virtual_Judge —— Binary Search Tree I Aizu - ALDS1_8_A.cpp created by VB_KoKing on 2019-05-09:18.
/* Procedural objectives:
Variables required by the program:
Procedural thinking:
Functions required by the program:
Determination algorithm:
Determining data structure:
*/
/* My dear Max said:
"I like you,
So the first bunch of sunshine I saw in the morning is you,
The first gentle breeze that passed through my ear is you,
The first star I see is also you.
The world I see is all your shadow."
FIGHTING FOR OUR FUTURE!!!
*/
#include <iostream>
#include <cstdlib>
using namespace std;
struct Node {
int key;
Node *right, *left, *parent;
};
Node *root, *NIL;
void insert(int k) {
Node *y = NIL;
Node *x = root;
Node *z;
z = (Node *) malloc(sizeof(Node));
z->key = k;
z->left = NIL;
z->right = NIL;
while (x != NIL) {
y = x;
if (z->key < x->key)
x = x->left;
else
x = x->right;
}
z->parent = y;
if (y == NIL)
root = z;
else {
if (z->key < y->key)
y->left = z;
else y->right = z;
}
}
//前序遍历
void pre_parse(Node *u) {
if (u == NIL) return;
cout << " " << u->key;
pre_parse(u->left);
pre_parse(u->right);
}
//中序遍历
void in_parse(Node *u) {
if (u == NIL) return;
in_parse(u->left);
cout << " " << u->key;
in_parse(u->right);
}
int main() {
int n;
string com;
cin >> n;
for (int i = 0; i < n; i++) {
cin >> com;
if (com == "insert") {
int x;
cin >> x;
insert(x);
} else if (com == "print") {
in_parse(root);
cout << endl;
pre_parse(root);
cout << endl;
}
}
return 0;
}