其实是比较简单的一道期望状压dp，考试时一直在想数组表示概率，然而最后出的数总是小于一，于是无奈的把第一个点判掉放弃了其他点。
设f[i]为状态为i时到全部买到的期望次数，$f[i]=∑f[j]*p[k]+（1-∑p[k]）+1$,f[（1<<n）-1]=0,倒着推，k为j中的元素，$i|（1<<(k-1)）=j$，然后可以用高斯消元求解（显然会T啊），其实只要移项就可以了，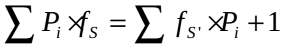
，时间复杂度：O(2^N)。
#include<iostream>
#include<cstdio>
#include<bitset>
#define int LL
#define LL long long
using namespace std;
double f[1<<22],sp;
int n,w[21],sum;
double p[21];
signed main()
{
// freopen("in.txt","r",stdin);
cin>>n;
for(int i=1;i<=n;i++)
{
cin>>p[i]>>w[i];sp+=p[i];sum+=w[i];
}
f[(1<<n)-1]=0;
for(int i=(1<<(n))-2;i>=0;i--)
{
double sum=0,spp=0;
for(int k=1;k<=n;k++)
if(((1<<(k-1))|i)!=i)
spp+=p[k],sum+=p[k]*f[i|(1<<(k-1))];
f[i]=(sum+1)/spp;
}
printf("%lld
%0.3lf
",sum,f[0]);
}
还有一点就是要用longlong,int会wa50，虽然算着只是擦边，但是这种情况还是开longlong比较好。