[CQOI2011]放棋子

C. 放棋子

 

题目描述

输入格式

输入第一行为两个整数n, m, c，即行数、列数和棋子的颜色数。
第二行包含c个正整数，即每个颜色的棋子数。
所有颜色的棋子总数保证不超过nm。
N,M<=30 C<=10 总棋子数有大于250的情况

输出格式

输出仅一行，即方案总数除以 1,000,000,009的余数。

样例

样例输入

4 2 2
3 1

样例输出

8

数据范围与提示

30% n,m<=10

一看这数据范围先想到了状压，然后就完戏了…

其实就是个dp，设f[i][j][k]为前k种棋子，放任意i行j列的方案数，设g[i][j][k]为用k个相同颜色的棋子放任意i行j列的方案数，

则f[i][j][k]=f[l][r][k-1]*g[i-l][j-r][num[k]]*C(n-l,i-l)*C(m-r,j-r);   1<=l<=i,1<=r<=j;

即用前k-1种放l行r列并将其固定在左上角，用第k种放剩下的i-l行，j-r列（从剩下的n-l行，m-r列中选）并将其平移固定（这样对dp是没有影响的）。

然后问题来了，g怎么算？

这里要用到一个小小的容斥，g[i][j][k]=C（i*j,k）-（k个相同颜色棋子未占满i行j列的情况数），

为什么是方形的i*j呢？因为黄色区域已经被前k-1种棋子占满，所以绿色区域不可能再放第k种棋子，此时第k中棋子能放的只有蓝色区域。

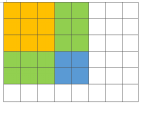
所以g[i][j][k]=C(i*j,k)-g[l][r][k]*C(i,l)*C(j,r);  1<=l<=i,1<=r<=j (l!=i || r!=j);

 ∑f[i][j][c]即为所求。

ps.组合数要打表啊，不然会T的……

#include<iostream>
#include<bitset>
#include<cstdio>
#include<cmath>
#define LL long long
#define int LL
#define mod 1000000009
using namespace std;
int n,m,c;LL num[15];
LL jc[910];
LL f[35][35][15],g[35][35][15];
LL C[950][950];
#define max(a,b) ((a)>(b)?(a):(b))
#define min(a,b) ((a)<(b)?(a):(b))

void get_C()
{
	C[0][0]=1;
	for(int i=1;i<=900;i++)
	{
		C[i][0]=1;
		for(int j=1;j<=900;j++)
			C[i][j]=(C[i-1][j]+C[i-1][j-1])%mod;
	}
}
#define C(n,m) C[n][m]
inline int read()
{
    int s=0;char a=getchar();
    while(a<'0'||a>'9')a=getchar();
    while(a>='0'&&a<='9'){s=s*10+a-'0';a=getchar();}
    return s;
}
signed main()
{
//    freopen("in.txt","r",stdin);
    
    n=read(),m=read(),c=read();
    for(int i=1;i<=c;i++)num[i]=read();
	get_C();

	for(int i=1;i<=n;i++)	
		for(int j=1;j<=m;j++)
			for(int o=1;o<=c;o++)
			if(i*j>=num[o])
			{
				for(int l=1;l<=i;l++)
					for(int r=1;r<=j;r++)
						if(l!=i||r!=j)
							g[i][j][o]=(g[i][j][o]+ g[l][r][o]*C(i,l)%mod*C(j,r)%mod )%mod;
				g[i][j][o]=( (C(i*j,num[o]) - g[i][j][o] )%mod+mod)%mod;
			}
	f[0][0][0]=1;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			for(int k=1;k<=c;k++)   
            {
				for(int l=0;l<=i;l++)
					for(int r=0;r<=j;r++)
						f[i][j][k]=( f[i][j][k] + f[l][r][k-1]*g[i-l][j-r][k]%mod*C(n-l,i-l)%mod*C(m-r,j-r)%mod )%mod;
            }
    LL ans=0;
	for(int i=1;i<=n;i++)
		for(int j=1;j<=m;j++)
			ans=(ans+f[i][j][c])%mod;
    printf("%lld
",ans%mod);
}