1.学习总结
1.1图的思维导图
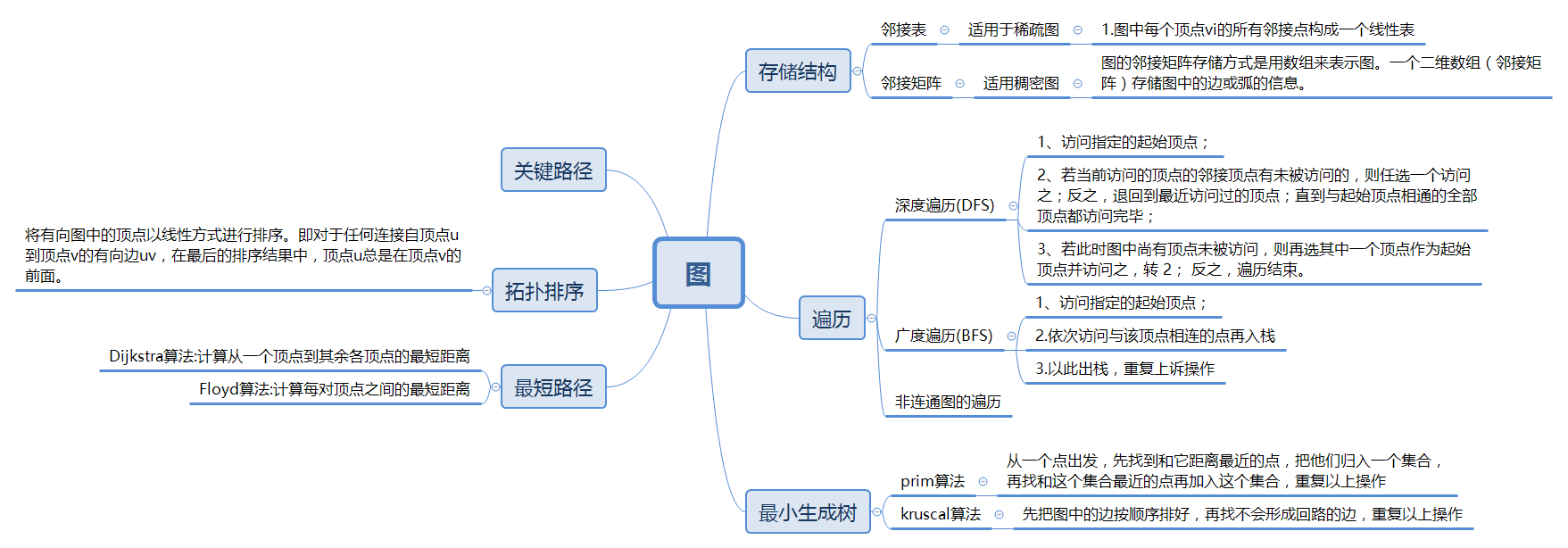
1.2 图结构学习体会
深度遍历算法
深度优先遍历,是对一个连通图进行遍历的算法。它的思想是从一个顶点V0开始,沿着一条路一直走到底,如果发现不能到达目标解,那就返回到上一个节点,然后从另一条路开始走到底,这种尽量往深处走的概念即是深度优先的概念。
广度遍历算法
广度优先遍历,也是对连通图遍历的算法。它的思想是从一个顶点V0开始,先遍历和它直接相连的点,再把这些点入栈,再从栈中取出点重复上述操作,这种尽可能多访问节点的概念就是广度优先遍历,深度优先和广度优先都是图常用的遍历算法,适用于不同情况。
Prim和Kruscal算法
这两种算法都是求图的最小生成树的算法,prim算法:从一个点出发,先找到和它距离最近的点,把他们归入一个集合,再找和这个集合最近的点再加入这个集合,重复以上操作。Kruscal算法:先把图中的边按顺序排好,再找不会形成回路的边,重复以上操作,我觉得prim算法会更好用一点
Dijkstra算法
用于求图中最短路径的算法,设G = (V,E)是一个带权有向图,把图中顶点集合V分成两组,第一组为已求出最短路径的定点集合(用S表示,初始时S中只有一个源点,以后每求得一条最短路径V,..,K,就将k加入集合S中,直到所有定点都加入S中,算法结束),第二组为其余未确定最短路径的顶点集合(用U表示),按最短路径长度的递增次序依次把第二组中顶点加入S
拓扑排序算法
设G = (V,E)是一个具有n个定点的有向图,V中顶点序列V1,V2,V3....Vn为一个拓扑序列并且当且仅当该顶点序列满足下列条件:若<V1,Vi>是图中的边,则在序列中V1在Vi之前,这样的过程叫做拓扑排序,拓扑排序有广泛的应用。
2.PTA实验作业
题目1:7-3 六度空间
设计思路
BFS(int v,int n,int e){
count表示六度空间访问点个数,last记录当前层最后一个元素
初始化visited数组
visited[v] = 1表示当前点已访问
初始化front = rear = -1 队列为空
V入栈
last = v记录当前层最后的点
while(队列不空)
V = 队首元素
for (i = 1 to i = n)
if(i未访问&&i于v点有边)
i入栈,visited[i] = 1,tail = i,count++
end if
if (v是单前层最后一个元素)level++,last = tail
end if
end while
return count
代码截图
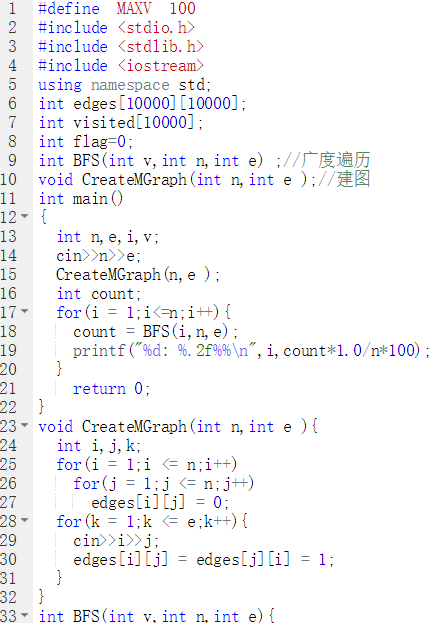
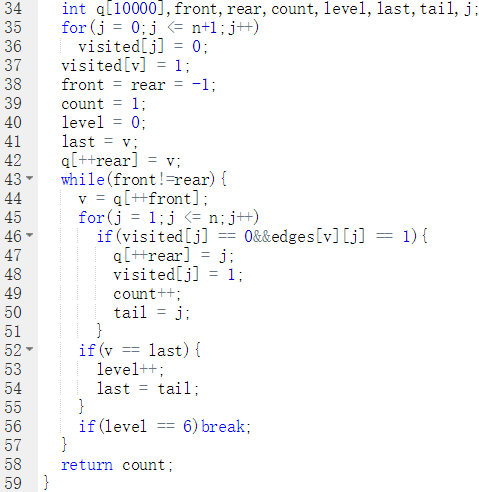
PTA提交列表说明

其中的段错误和部分错误都是因为数组定义的不够大,这一题难就难在判断他的层数,当时也是看了百度的
代码才懂得用last记录当前层最后一个点
题目2:7-4 公路村村通
设计思路
int prim(MGraph g){
lowcost数组记录和其他点最近距离,cost记录总成本
lowcost[1] = 0出发点本身距离不存在,记为0
for(i = 2 to i = g.n)
lowcost[i] = g.edges[1][i]初始点的最近距离
end for
for(i = 2 to i= g.n)
min = 100001
while(j<=g.n)
if(路径存在&&路径<min)
min = lowcost[j];
k = j;
if(找不到最近的点)return -1
cost+=min
lowcost[k] = 0表示k点加入该集合
修正lowcost数组判断新加入的点是否有
与未加入集合点更近的
}
代码截图
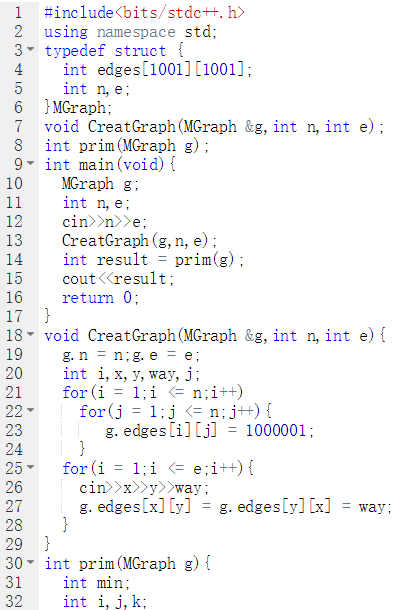
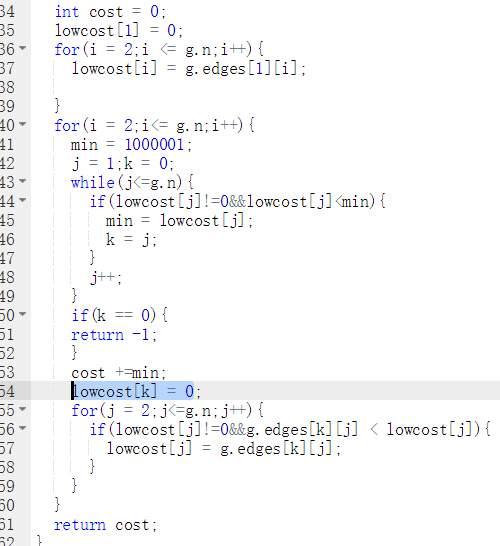
PTA提交列表说明

部分正确是在建表的时候吧不存在的边赋值为0,这是不对的,改了之后就正确了
题目3:7-7 旅游规划
设计思路
void Dijkstra(int v,int n,int e,int end){
定义dist数组存放距离path数组存放路径cost数组存放消费
定义s数组存放加入集合的点
先初始化这几个数组
将V加入s数组,path[v] = 0
mindis = INF;
for(j = 0 to j < n)
if(j未加入集合且dist[j]存在)
u = j;
mindis = dist[j];
end if
end for
s[u] = 1;
for(j = 0 to j < n)
if(j加入 集合)
if(新加入点距离比原来近)
更新dist[j],path[j],cost[j]
else if(新加入点距离和原来一样近但比较便宜)
更新dist[j],path[j],cost[j]
代码截图
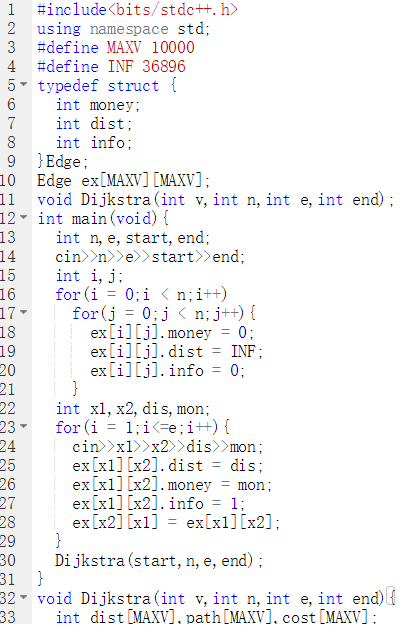
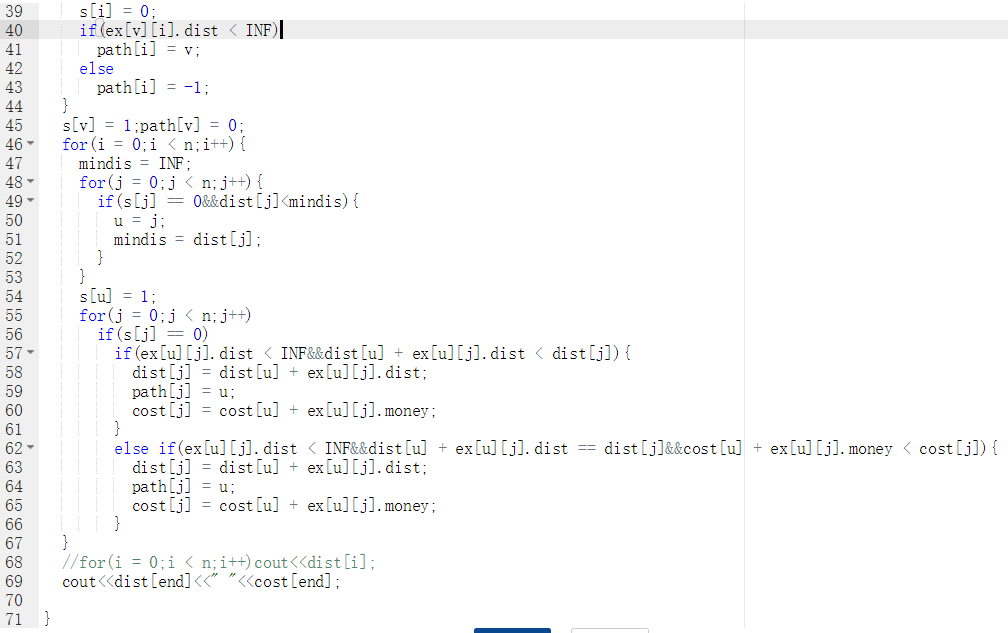
PTA提交列表说明

部分正确是因为没有把不存在的边等于INF,导致后续比较会出现问题
3.截图本周题目集的PTA最后排名
3.1 PTA排名

3.2 我的总分244
4. 阅读代码
贝尔曼-福特算法

贝尔曼-福特算法与迪杰斯特拉算法类似,迪杰斯特拉算法以贪心法选取未被处理的具有最小权值的节点,然后对其的出边进行操作;而贝尔曼-福特算法简单地对所有边进行操作,我觉得迪杰斯特拉算法更好一点,但贝尔曼-福特算法也不失为一种好思路