[学习笔记]μ函数

省队集训看着台上的老师讲了一上午的莫比乌斯反演，整个人都是懵的，因为我看不清黑板和投影！！！

回家后本来想晚上自学完的，却奈何自己是个拖延症患者，只敲了μ函数(说多了都是泪QAQ)

代码的思路如下：

1.算质因数个数时因为有将1算上，所以每次都需要将符号取反；

2.为什么这样做能算出μ(a)=0呢？证明如下(如果有错可以指出，但别打我QAQ)：

  ①先证明：已知a=p₁×p₂×p₃×...×p_n×p_i(1<=i<=n且p为质数)

    则μ(a)=Σμ(i)(1<=i<=n)+Σμ(p_ip_j)(1<=i<j<=n)(为什么不列举μ(pi²×...)呢？因为它的值是0，不影响结果)

    可以发现，上式中μ()值为±1的各有n个(因为μ(p_i²)=0)，相抵消一下，μ(a)就等于0了。

  ②其次再证明：已知a=p₁^b_1×p₂^b_2×p₃^b₃×...×p_n^b_n(b_i≠0且max(b_i)>1)且μ(a)=0

    则令a'=p₁^b₁×p₂^b₂×p₃^b₃×...×p_n^b_n×p_i(1<=i<=n)

    μ(a')=μ(a)=0，因为它们满足μ(j)≠0的因数j是一样的，所以μ()值也是一样的。

3.最后证明|μ(i)|=1时，它的符号是正确的。

  已知a=p₁p₂p₃...p_np_n+1,a'=p₁p₂p₃...p_n,
  因为每次确定μ()时，都会对它的符号取反，所以μ(a')=-Σi(i|a且i≠a)，即μ(a')+Σi(i|a且i≠a)=0。
  设x=μ(p_n+1)+Σμ(p_n+1p_i)(1<=i<=n)+Σμ(p_n+1p_ip_j)(1<=i<j<=n)+Σμ(p_n+1p_ip_jp_k)(1<=i<j<k<=n)+...
  (x表示将p_n+1分别跟p₁-p_n中0、1、2、...(n-1)个不同的素数组合而成的μ值的和),则x=Σ(-1)ⁱ⁺¹×c(i,n)(0<=i<=n-1)。
  所以-μ(a)=x，即μ(a)=-x。
  设x'=Σ(-1)ⁱ⁺¹×c(i,n)(0<=i<=n)，

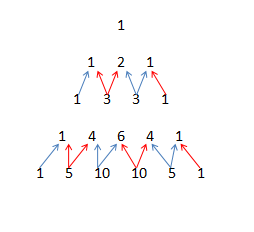
  观察杨辉三角形得
  Σc(2i,n)(1<=i<=n/2)=Σc(2i+1,n)(0<=i<=(n-1)/2)=上一行所有数之和(如图箭头所示)，正负互相抵消，故x'=0。
  所以x=x'-(-1)ⁿ⁺¹×c(n,n)=-(-1)ⁿ⁺¹。
  即μ(a)=-x=(-1)ⁿ⁺¹，符合μ函数定义。

时间复杂度：O(nlogn) 

#define N 10000001

int mu[N],n;
inline void get_mu(){
    for(int i=1;i<=n;i++){
        if(i==1) mu[i]=1;
        else mu[i]=0-mu[i];
        for(int j=i<<1;j<=n;j+=i)
            mu[j]+=mu[i]; 
    }
}