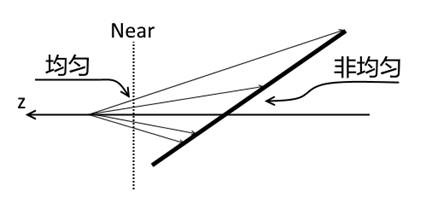
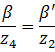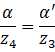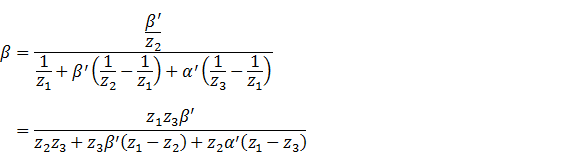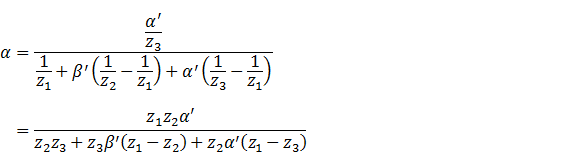许多着色方法都要用到顶点间的线性插值,譬如逐像素着色的Phong Shading往往需要进行纹理坐标等的线性插值。然而,透视投影会导致直接在屏幕空间进行线性插值得到的结果不正确,如下图:
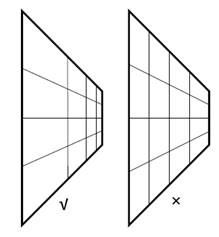
在屏幕上进行的线性插值并不对应在物体上的线性插值,这将导致一系列与该插值相关的着色结果出现错误。譬如,如果在屏幕上直接插值纹理坐标,会得到下图中右边的结果(左边为正确的结果):
解决该问题的一种方式是利用![]() 在屏幕空间的线性性。假设坐标为
在屏幕空间的线性性。假设坐标为![]() 和
和![]() 的点分别被投影到屏幕上坐标为
的点分别被投影到屏幕上坐标为![]() 和
和![]() 的位置,直线
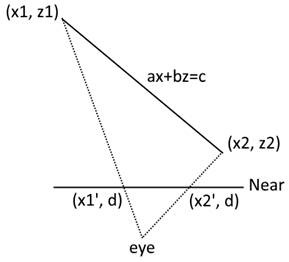
的位置,直线![]() 的方程为
的方程为![]() ,如下图:
,如下图:
整理得
类似地,有以下方程成立:
类似的式子对![]() 上的每一点及其投影点都成立。现考虑在
上的每一点及其投影点都成立。现考虑在![]() 和
和![]() 间进行的线性插值
间进行的线性插值![]() ,有:
,有:
由此可知,在屏幕上进行的线性插值对应于在投影前空间中对![]() 的线性插值。现假设要在
的线性插值。现假设要在![]() 和
和![]() 间对属性值
间对属性值![]() 和
和![]() 进行线性插值得到
进行线性插值得到![]() ,易知——
,易知——
整理得
这就得到了正确的对![]() 插值的方法:在屏幕空间中对
插值的方法:在屏幕空间中对![]() 、
、![]() 分别进行线性插值得到
分别进行线性插值得到![]() 和
和![]() ,然后用后者除以前者,即得到
,然后用后者除以前者,即得到![]() 。
。
以上推导仅考虑了![]() 、
、![]() 坐标,现考虑三角形
坐标,现考虑三角形![]() 上进行的线性插值,假设屏幕上线性插值的权重为
上进行的线性插值,假设屏幕上线性插值的权重为![]() 和
和![]() ,真实三角形上对应的权重为
,真实三角形上对应的权重为![]() 和
和![]() ,故有
,故有
解得
这就得到了根据![]() 求出
求出![]() 的公式。由于在透视投影变换后、坐标齐次化之前,
的公式。由于在透视投影变换后、坐标齐次化之前,![]() 和
和![]() 的比值是一定的,因此上面两个公式中的
的比值是一定的,因此上面两个公式中的![]() 坐标均可换成透视投影变换后、坐标齐次化之前对应的
坐标均可换成透视投影变换后、坐标齐次化之前对应的![]() 坐标。
坐标。
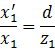
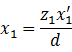
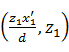
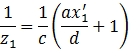
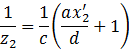
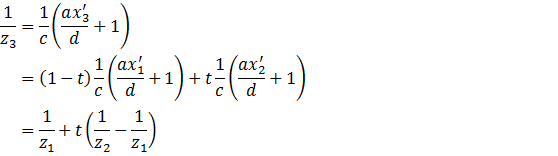
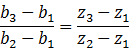
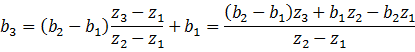
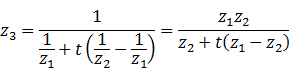
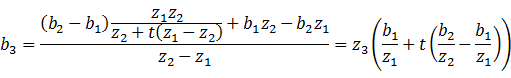
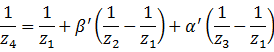
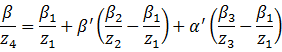
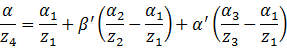
![clip_image082[1] clip_image082[1]](https://images2015.cnblogs.com/blog/1085776/201612/1085776-20161231212534789-528400296.gif)