【题目描述】
现有N个城市,城市之间有道路相连,一共有M条双向道路,保证没有自环和重边。
现有K个城市已经被僵尸控制,所以不能进入。若某个正常城市到某个僵尸城市的距离不超过S,则称此城市为危险城市。
小A住在1号城市,他想去N号城市避难,这两座城市没有被侵略。白天小A会走一段道路,晚上要住在所处城市。在正常城市需花费P元,而在危险城市,由于安保措施,所以会变贵,为Q元。所有危险城市的住宿花费相同,正常城市也是如此。且在1号城市和N号城市,小A不需要住店。
现询问从1号城市到N号城市所需要的最小花费,数据保证存在路径可以成功逃离。
【输入描述】
第一行输入4个整数N、M、K、S;
第二行输入2个整数P、Q;
接下来K行,每行输入1个整数Ci,表示僵尸控制的城市;
接下来M行,每行输入2个整数Ai、Bi,表示一条无向边。
【输出描述】
输出一个整数表示最低花费。
【输入样例】
13 21 1 1
1000 6000
7
1 2
3 7
2 4
5 8
8 9
2 5
3 4
4 7
9 10
10 11
5 9
7 12
3 6
4 5
1 3
11 12
6 7
8 11
6 13
7 8
12 13
【输出样例】
11000
【数据范围及提示】
样例如图所示:
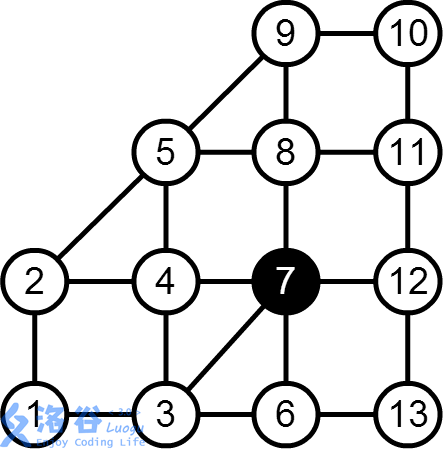
对于20%数据,N <= 50;
对于100%数据,2 <= N <= 100000,1 <= M <= 200000,0 <= K <= N-2,0 <= S <= 100000,1 <= P < Q <= 100000。