1.字符串匹配
看到题目以为真是字符串题结果是数学题。。70分做法很傻逼然而我更傻逼只有30。。。
正解是发现两个位置会匹配当且仅当mod gcd(lena,lenb)同余,在一个lcm(lena,lenb)的长度内所有模gcd同余的位置会一一匹配。我大概只能感性理解一下和随便证一下模gcd同余则可以匹配。
然后用乘法原理计数。代码超短的。

1 //Achen
2 #include<algorithm>
3 #include<iostream>
4 #include<cstring>
5 #include<cstdlib>
6 #include<vector>
7 #include<cstdio>
8 #include<queue>
9 #include<cmath>
10 #include<set>
11 #include<map>
12 #define Formylove return 0
13 #define For(i,a,b) for(int i=(a);i<=(b);i++)
14 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
15 const int N=2e6+7;
16 typedef long long LL;
17 typedef double db;
18 using namespace std;
19 int n,m,cnt[30],lena,lenb;
20 LL ans;
21 char a[N],b[N];
22
23 template<typename T>void read(T &x) {
24 char ch=getchar(); x=0; T f=1;
25 while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
26 if(ch=='-') f=-1,ch=getchar();
27 for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0'; x*=f;
28 }
29
30 LL gcd(LL a,LL b) { return !b?a:gcd(b,a%b); }
31
32 #define ANS
33 int main() {
34 #ifdef ANS
35 freopen("string.in","r",stdin);
36 freopen("string.out","w",stdout);
37 #endif
38 read(n); read(m);
39 scanf("%s",a); lena=strlen(a);
40 scanf("%s",b); lenb=strlen(b);
41 LL d=gcd(lena,lenb);
42 For(t,0,d-1) {
43 memset(cnt,0,sizeof(cnt));
44 For(i,0,lena/d-1)
45 cnt[a[i*d+t]-'a']++;
46 For(i,0,lenb/d-1)
47 ans+=cnt[b[i*d+t]-'a'];
48 }
49 ans*=n*d/lenb;
50 printf("%lld
",ans);
51 Formylove;
52 }
2.积木大赛
感觉这题很傻逼啊。少有的不是模板但是可以秒切的题。
枚举最高点的位置,二分最高点,再往左右二分满足最高点条件(从最高点开始依次减1)的最近位置,这个可以用st表或者线段树什么的维护。算算要达到最高点积木够不够即可。

1 //Achen
2 #include<algorithm>
3 #include<iostream>
4 #include<cstring>
5 #include<cstdlib>
6 #include<vector>
7 #include<cstdio>
8 #include<queue>
9 #include<cmath>
10 #include<set>
11 #include<map>
12 #define Formylove return 0
13 #define For(i,a,b) for(int i=(a);i<=(b);i++)
14 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
15 const int N=100005;
16 typedef long long LL;
17 typedef double db;
18 using namespace std;
19 int n,m;
20 LL h[N],st1[N][17],st2[N][17],sum[N],ans;
21
22 template<typename T>void read(T &x) {
23 char ch=getchar(); x=0; T f=1;
24 while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
25 if(ch=='-') f=-1,ch=getchar();
26 for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0'; x*=f;
27 }
28
29 void make_st() {
30 For(i,1,n) st1[i][0]=h[i]+i,st2[i][0]=h[i]+(n-i+1);
31 For(j,1,16) For(i,1,n) {
32 if(i+(1<<j)-1<=n)
33 st1[i][j]=max(st1[i][j-1],st1[i+(1<<j-1)][j-1]);
34 if(i-(1<<j)+1>=1)
35 st2[i][j]=max(st2[i][j-1],st2[i-(1<<j-1)][j-1]);
36 }
37 }
38
39 int ck(int pos,LL x) {
40 int l=pos,r=pos;
41 Rep(i,16,0) if(r+(1<<i)-1<=n&&st1[r][i]<x+pos)
42 r+=(1<<i);
43 Rep(i,16,0) if(l-(1<<i)+1>=1&&st2[l][i]<x+(n-pos+1))
44 l-=(1<<i);
45 LL nd=0;
46 if(l<1||r>n) return 0;
47 if(l+1<=pos) {
48 l++;
49 nd=nd+(x+x-(pos-l))*(pos-l+1)/2-(sum[pos]-sum[l-1]);
50 }
51 if(r-1>=pos) {
52 r--;
53 nd=nd+(x+x-(r-pos))*(r-pos+1)/2-(sum[r]-sum[pos-1]);
54 }
55 return nd-(x-h[pos])<=m;
56 }
57
58 LL solve(int pos) {
59 LL l=h[pos],r=h[pos]+m,rs=l;
60 while(l<=r) {
61 int mid=((l+r)>>1);
62 if(ck(pos,mid)) rs=mid,l=mid+1;
63 else r=mid-1;
64 }
65 return rs;
66 }
67
68 #define ANS
69 int main() {
70 #ifdef ANS
71 freopen("block.in","r",stdin);
72 freopen("block.out","w",stdout);
73 #endif
74 read(n); read(m);
75 For(i,1,n) read(h[i]),sum[i]=sum[i-1]+h[i];
76 make_st();
77 For(i,1,n)
78 ans=max(ans,solve(i));
79 printf("%lld
",ans);
80 Formylove;
81 }
3.考古研究
30分和70分还是比较好做,但是傻逼地搞了好久t1然后这天考得就很爆炸。
一张我的草稿:
就是草稿,所以非常乱。
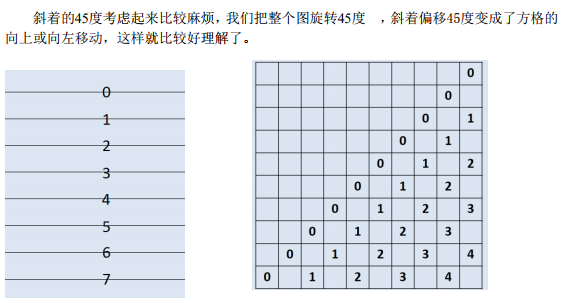
继续70分是思路,倒着考虑最后地表的每个点经过若干次沉降后到达的位置。
对于这个转过的网格图,从左到右x从1~n,从上到下y从1~n,每个格子上的权值就是它的x坐标减y坐标除以2
操作逆过来,一种是选x较大的一部分区间x+=2*L,一种是选y较小的部分区间y-=2*L
每次操作线段树上二分在操作范围内的区间,区间修改即可。直接二分好写很多就没写线段树上二分了。


1 //Achen
2 #include<algorithm>
3 #include<iostream>
4 #include<cstring>
5 #include<cstdlib>
6 #include<vector>
7 #include<cstdio>
8 #include<queue>
9 #include<cmath>
10 #include<set>
11 #include<map>
12 #define Formylove return 0
13 #define For(i,a,b) for(int i=(a);i<=(b);i++)
14 #define Rep(i,a,b) for(int i=(a);i>=(b);i--)
15 const int N=200007;
16 typedef long long LL;
17 typedef double db;
18 using namespace std;
19 int n,m;
20
21 template<typename T>void read(T &x) {
22 char ch=getchar(); x=0; T f=1;
23 while(ch!='-'&&(ch<'0'||ch>'9')) ch=getchar();
24 if(ch=='-') f=-1,ch=getchar();
25 for(;ch>='0'&&ch<='9';ch=getchar()) x=x*10+ch-'0'; x*=f;
26 }
27
28 struct node {
29 int x,d,l;
30 }q[N];
31
32 #define lc x<<1
33 #define rc (x<<1|1)
34 #define mid ((l+r)>>1)
35 struct sgtree {
36 LL lz[N<<2];
37 void down(int x) {
38 if(!lz[x]) return ;
39 lz[lc]+=lz[x]; lz[rc]+=lz[x];
40 lz[x]=0;
41 }
42
43 void update(int x,int l,int r,int ql,int qr,int v) {
44 if(l>=ql&&r<=qr) {
45 lz[x]+=v; return ;
46 }
47 down(x);
48 if(ql<=mid) update(lc,l,mid,ql,qr,v);
49 if(qr>mid) update(rc,mid+1,r,ql,qr,v);
50 }
51
52 LL qry(int x,int l,int r,int pos) {
53 if(l==r) return lz[x];
54 down(x);
55 if(pos<=mid) return qry(lc,l,mid,pos);
56 else return qry(rc,mid+1,r,pos);
57 }
58 }sgx,sgy;
59
60 #define ANS
61 int main() {
62 #ifdef ANS
63 freopen("geologic.in","r",stdin);
64 freopen("geologic.out","w",stdout);
65 #endif
66 read(n); read(m);
67 For(i,1,m) {
68 read(q[i].x);
69 read(q[i].d);
70 read(q[i].l);
71 }
72 For(i,1,n) sgx.update(1,1,n,i,i,i),sgy.update(1,1,n,i,i,i);
73 Rep(i,m,1) {
74 if(q[i].d==1) { //down
75 int l=1,r=n,rs=-1;
76 while(l<=r) {
77 if(sgx.qry(1,1,n,mid)<=q[i].x) rs=mid,l=mid+1;
78 else r=mid-1;
79 }
80 if(rs!=-1) sgy.update(1,1,n,1,rs,-2*q[i].l);
81 }
82 else { //right
83 int l=1,r=n,rs=-1;
84 while(l<=r) {
85 if(sgy.qry(1,1,n,mid)>q[i].x) rs=mid,r=mid-1;
86 else l=mid+1;
87 }
88 if(rs!=-1) sgx.update(1,1,n,rs,n,2*q[i].l);
89 }
90 }
91 For(i,1,n) printf("%lld
",(sgx.qry(1,1,n,i)-sgy.qry(1,1,n,i))/2);
92 Formylove;
93 }
