codeforces906 D

题目链接：http://codeforces.com/contest/906/problem/D

题意：

　　给你n个数，再给你l~r，求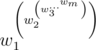%m

题解：

　　一开始不会

　　后来查到了欧拉降幂定理：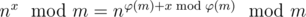

　　然后就会了

　　这样的话，每次从左往右求ans就变成了不断求n^x%m,依次往右递归即可。

代码

　　

#include <bits/stdc++.h>
using namespace std;
typedef long long ll;
#define N 100010
int i,j,k,n,x,y,t,q;
ll a[N],m;
map <ll,ll> f;
ll jisuan(ll n){
    if (f.count(n))return f[n];
    ll ans = n, z = n;for (ll i = 2; i * i <= n; ++i){if (n % i == 0){ans -= ans / i;while (n % i == 0) n /= i;}}
    if (n > 1) ans -= ans / n;return f[z] = ans;
}
ll Pow(ll a,ll b,ll mod){
    ll ret = 1;ll fl  = a >= mod;
    for (; b; b >>= 1){if (b & 1){ret *= a;if (ret >= mod) fl = 1, ret %= mod;}a *= a;if (a >= mod) a %= mod, fl = 1;}
    return ret + fl * mod;
}
ll solve(int l, int r,ll mod){if (l == r) return a[l];if (mod == 1) return 1;return Pow(a[l], solve(l + 1, r, jisuan(mod)), mod);}
int main(){
    scanf("%d%lld",&n,&m);
    for (int i=1;i<=n;++i)scanf("%lld",&a[i]);
    scanf("%d",&q);
    while (q--){scanf("%d%d",&x,&y);printf("%lld
",solve(x, y, m)%m);}
    return 0;
}