定义状态数组dp[i]表示以i为根节点,可以走的最远距离,也可以理解为以i为根节点树的高度。
我们考虑树的直径,
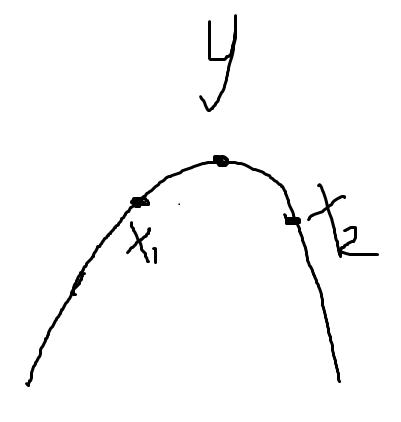
假设y是直径上的一个端点,X1和x2均为y的儿子节点,我们通过回溯的思想最先求出的应该是dp[x1],此时的dp[y]=0,然后下一步更新直径的长度,maxlen=max(maxlen,dp[y]+dp[x1]+val1)(val表示的是x1和y之间的距离),然后再更新dp[y]=dp[x1]+val1,接着回溯x2的值,dp[x2]被求出,注意在回溯x1的值的时候,dp[y]已经被求出来了即dp[x1]+val1,我们再更新直径的时候maxlen=max(maxlen+dp[y]+dp[x2]+val2),其实就相当于maxlen=max(maxlen,dp[x1]+val1+dp[x2]+val2); 也就是整个弯链的长度。
code:
void dfs(int x,int pa){ for(int i=head[x];i;i=edge[i].nxt){ int y=edge[i].to; if(pa==y) continue ; dfs(y,x); maxlen=max(maxlen,dp[x]+dp[y]+edge[i].val); dp[x]=max(dp[x],dp[y]+edge[i].val); } }
注意这里的
maxlen=max(maxlen,dp[x]+dp[y]+edge[i].val);
dp[x]=max(dp[x],dp[y]+edge[i].val);
前后顺序有讲究,防止出现maxlen=dp[x1]+dp[x1]+val这种情况