网络流初识一 （Ford-Fulkerson算法求最大流）

看了一个下午的最大流问题，首先要明白最大流是用来干嘛的。直观来说，流就像它的名字一样，从源头s运送一些“东西”到汇聚点t，比如下水道系统运输水流，公路网络运输车流。最大流就是求运输的“东西”的最大值。在运输的过程中，每条边都要有个权值c(i，j)，用来表示的是该边i-->j的可以承受的最大运输量。  所以每条边的运输量都要小于c(i，j)，并且除了源点和汇点外的每个点都应该满足流入的流量和 = 流出的流量和。

Ford-Fulkerson算法实现步骤

　　（1）找到满足各个流量限制的从s到t的一条路径，累加当前流量。

　　（2）构造残留网络，回到（1）。

　　（3）如果找不到一条从s到t的路径，那么算法结束。

　　关于残留网络：

　　　　比如说当前我找到了一条从s到t的路径，当前路径对应的流量为s，每条边对应的流量为flow(i，j)。如果说从s->t的路径经过了（i，j）这条路径，那么cf(i，j)=c(i，j) - flow(i，j)，其中cf(i，j)表示的是新的残留网络图中的流量限制。然后反向边cf(j,i)=cf(j,i)+flow(i,j)，为什么要让反向边加上对应的流量呢？就是为了修改之前的错误路径。比如下面这个图：

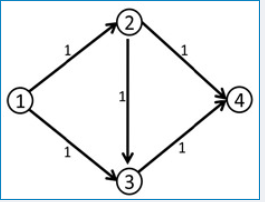
 从1到4的最大流显然是应该是2，1--2--4和1---3---4。

如果找到的路径是1---2---3---4，接下来图就变成了这样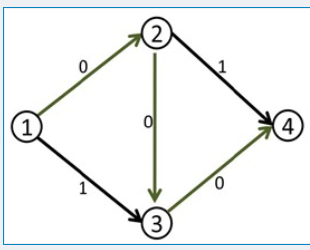

显然由于第一步的路径，我们不能再找到从1到4的路径。这样求出来的最大流就是1了。

但是如果构建反向图：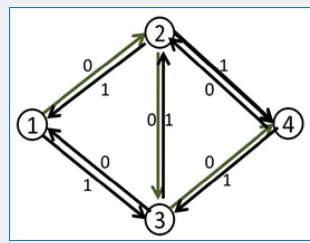

从1到4我们还可以找到一条新的路径1---3---2---4,。即第一次路径为1--2---3---4，第二次找的路径为1---3---2---4。第一次从2流到了3，第二次从反了回去，是不是就不经过相当于2--3这条路径呢？也就是和1--2--4+1---3---4等价。

网络流中还设计了一个名词：增广路径。其实增广路径就是在残留网络中寻找一条从s到t的一条路径。如果找不到，算法结束。

核心code:

class stu{
    public:
        int y,c,rev;//终点，权值，x在y中的位置(ve[y][rev]表示从y到x这条边) 
        stu(int x2,int x3,int x4){
            y=x2,c=x3,rev=x4;
        }
};
bool mark[N];
vector<stu>ve[N];
int dfs(int v,int t,int f){
    if(v==t) return f;
    mark[v]=1;
    for(int i=0;i<ve[v].size();i++){
        if(mark[ve[v][i].y]) continue ;
        if(ve[v][i].c<=0) continue ;
        int d=dfs(ve[v][i].y,t,min(ve[v][i].c,f));//求边v到ve[v][i].y的流量。
        if(d>0){
            ve[v][i].c-=d;
            ve[ve[v][i].y][ve[v][i].rev].c+=d;
            return d;     
        }
    }
    return 0;
}
int Ford-Fulkerson(){
    int flow=0; 
    while(1){
        memset(mark,0,sizeof mark);
        int f=dfs(s,t,INF);
        if(f==0) break; 
        flow+=f;
    }    
    return flow;
}

注：看了好久关于最大流的东西，纯属个人理解。