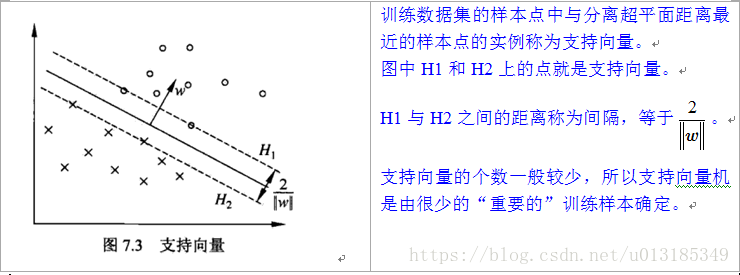
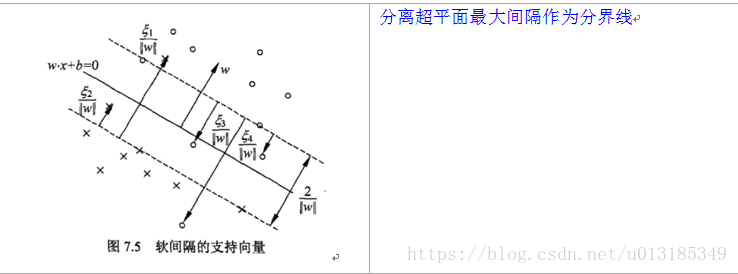
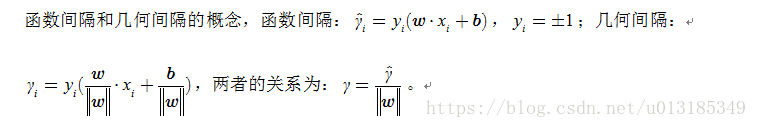SVM(Support Vector Machine),支持向量机,有监督学习模型,一种分类模型。在特征空间(输入空间为欧式空间或离散集合,特征空间为欧式空间或希尔伯特空间)中寻找间隔最大化的分离超平面的线性分类器。学习策略就是间隔最大化,可形式化为一个求解凸二次规划(QP)的问题,也等价于正则化的合页损失函数的最小化问题。
针对数据特点,处理方法或者说原理是:
(1).当训练样本线性可分时,通过硬间隔最大化,学习一个线性分类器,即线性可分SVM;
(2).当训练数据近似线性可分时,引入松弛变量,通过软间隔最大化,学习一个线性分类器,即线性支持向量机;
(3).当训练数据线性不可分时,通过使用核技巧及软间隔最大化,学习非线性支持向量机。
一句话解释一下线性核和高斯核的区别:
Linear核主要用于线性可分的情形,参数少,速度快;高斯核主要用于线性不可分的情形,参数多,分类结果依赖于参数,可通过公式辨别。
1. 如果Feature的数量很大,跟样本数量差不多,这时候选用LR或者是LinearKernel的SVM
2. 如果Feature的数量比较小,样本数量一般,不算大也不算小,选用SVM+Gaussian Kernel
3. 如果Feature的数量比较小,而样本数量很多,需要手工添加一些feature变成第一种情况
当样本在原始空间线性不可分时,将样本由原始空间映射到一个更高维的特征空间,使得样本在这个特征空间内线性可分。(高维空间线性可分)
通过核函数可以学习非线性支持向量机,等价于隐式地在高维的特征空间中学习线性支持向量机。即传说中的核方法。
为什么SVM对缺失数据敏感?
SVM没有处理缺失值的策略(决策树有),SVM希望样本在特征空间中线性可分,所以特征空间的好坏对SVM性能很重要。
为什么使用间隔最大化:
线性可分支持向量机利用间隔最大化求得最优分离超平面,这时,解是存在且唯一的。另一方面,此时的分隔超平面所产生的分类结果是最鲁棒的,对未知实例的泛化能力最强。
为什么将SVM的原始问题转换为其对偶问题来解决:
因为对偶问题往往更容易求解,原问题的求解包含约束条件,使问题求解变得复杂,将目标函数和约束重新整合到一个新函数,即拉格朗日函数,然后再通过这个函数来寻找最优解比较容易。
具体求解过程见李航统计学习方法第七章。
SVM用到的Python库和调参:
Sklearn库,调用sklearn.svm,-c 惩罚参数;kernel:0为线性,1为多项式,2为RBF核,3为sigmoid(tanh);gamma:核函数参数;coef0:核函数的常数项。
https://www.zhihu.com/question/21094489上的例子解释的很通俗易懂。
<script>
(function(){
function setArticleH(btnReadmore,posi){
var winH = $(window).height();
var articleBox = $("div.article_content");
var artH = articleBox.height();
if(artH > winH*posi){
articleBox.css({
'height':winH*posi+'px',
'overflow':'hidden'
})
btnReadmore.click(function(){
articleBox.removeAttr("style");
$(this).parent().remove();
})
}else{
btnReadmore.parent().remove();
}
}
var btnReadmore = $("#btn-readmore");
if(btnReadmore.length>0){
if(currentUserName){
setArticleH(btnReadmore,3);
}else{
setArticleH(btnReadmore,1.2);
}
}
})()
</script>
</article>