线性最小二乘法（附MATLAB代码）

本文部分转载自优化算法交流地的文字，转载仅作学习使用。

用n次多项式拟合给定数据.
注意:对于非线性曲线,例如指数曲线(y=a_{1}e^{a_{2}x}),拟合前需做变量代换,化为对(a_1,a_2)的线性函数.
本文主要从如何使用MATLAB实现最小二乘法，首先给出今天重点使用的两个函数。

p=polyfit(x,y,n)：最小二乘法计算拟合多项式系数。x，y为拟合数据向量，要求维度相同，n为拟合多项式次数。返回p向量保存多项式系数，由最高次向最低次排列。y=polyval(p,x)：计算多项式的函数值。返回在x处多项式的值，p为多项式系数，元素按多项式降幂排序。　

比如拟合下面这组数据

x=[9,13,15,17,18.6,20,23,29,31.7,35];
y=[-8,-6.45,-5.1,-4,-3,-1.95,-1.5,-0.4,0.2,-0.75];

先用matlab将这组离散点画出来，

plot(x,y,'o')

---

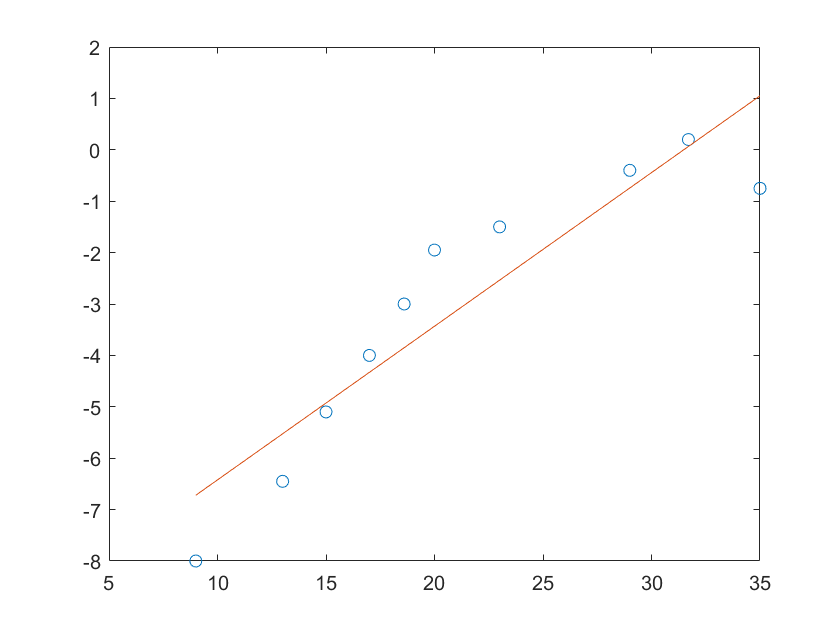
嗯，大概这个样子，这时我们想使用一次函数拟合上述曲线，可使用以下代码

clear
clc
x=[9,13,15,17,18.6,20,23,29,31.7,35];
y=[-8,-6.45,-5.1,-4,-3,-1.95,-1.5,-0.4,0.2,-0.75];
coefficient=polyfit(x,y,1);  %用一次函数拟合曲线，想用几次函数拟合，就把n设成那个数
y1=polyval(coefficient,x);
plot(x,y,'o',x,y1,'-')

得到的结果是

coefficient=[0.2989,-9.4107]

所以得到的一次函数为

y=0.2989*x-9.4107

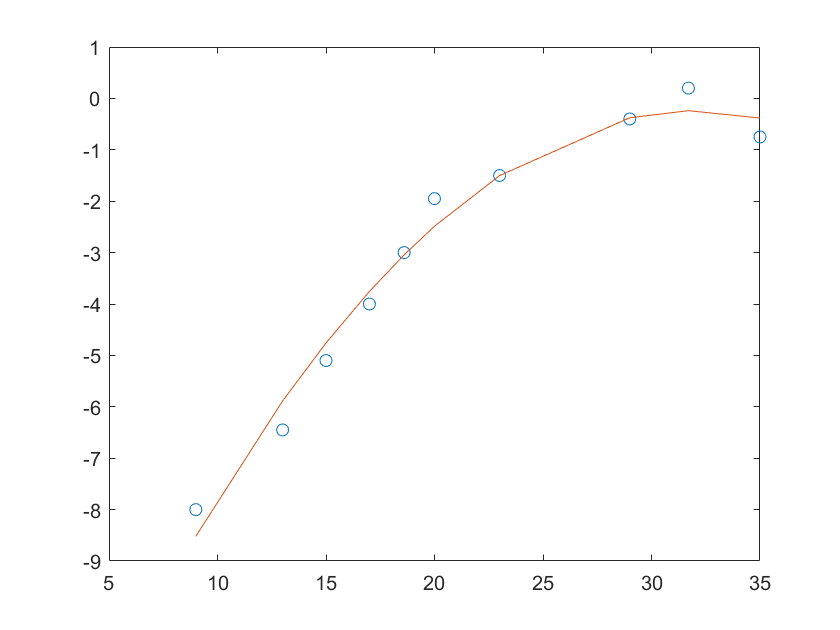
同理如果用二次函数拟合该曲线，得到的各项系数为

coefficient=[-0.0157 1.0037 -16.2817]

所以得到的二次函数为

y=-0.0157*x^2+1.0037*x-16.2817

其他阶数依此类推。
但是使用polyfit(x,y,n)函数有一个注意事项：

向量x（其中元素作为自变量）中不重复的元素个数m，和拟合阶数k需要满足m>=k+1.简单分析：k阶拟合需要确定k+1个未知参数（如1阶拟合y = ax + b需要确定a和b两个参数），故而至少需要k+1个方程，故而需要至少k+1个不同的已知数对（x，y），由于函数中x只能对应一个y，故而需要至少k+1个不同的x　
举个例子，比如说我们想用9阶多项式拟合上述曲线时，我们发现拟合的曲线是正常的，得到的各项系数也是正常的　

　

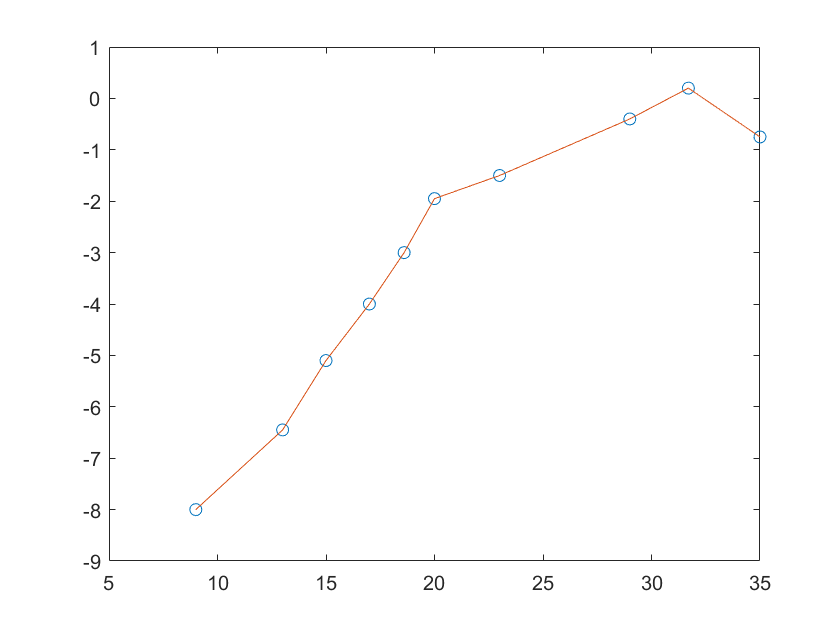
但是当我们用10阶多项式拟合曲线时，此时各项系数如下，得到的曲线如下　
　　

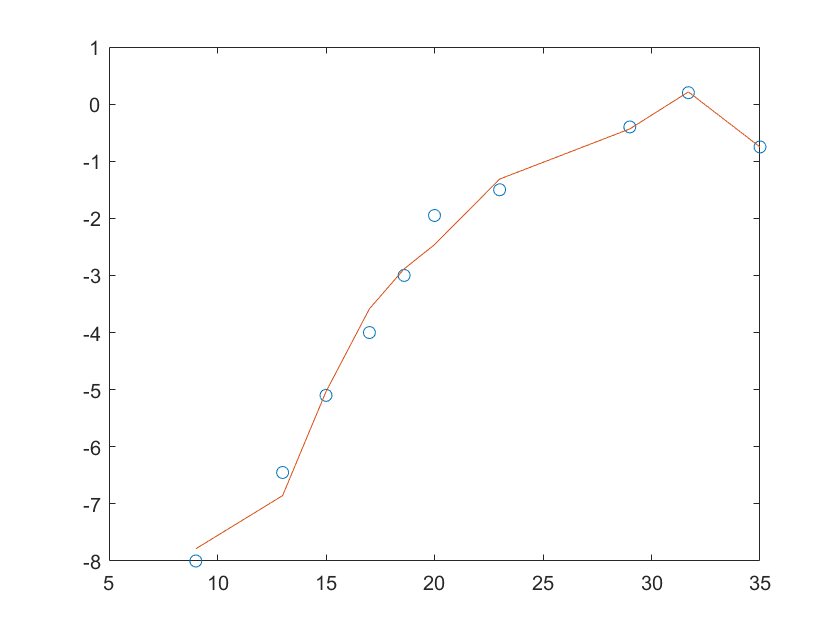
很明显出现了问题，所以使用polyfit(x,y,n)函数时要严格遵守上述事项。