题意描述
- 给定你一个长为 n 的序列 A ,请问要在这个序列中擦除多少个数(这些数字共同组成了序列A的一段前缀),才能使这个序列是一个好的序列。即擦除序列A的一段前缀,使擦除后的序列是一个好的序列。求被擦除前缀中数字的个数。
- 对好的序列的定义:假定有一个序列 B,你可以每次从序列的首项或末项取出一个数字放在序列 C 的末尾。假如存在一种方案使得 C 不降,那么 B 就是好的序列。
- 本题有 T 组数据。1(leq)T(leq) 2 X(10^4) ;1(leq) (sum)n (leq) 2 X(10^5) 。
输入描述
The first line of the input contains one integer t — the number of test cases.
The first line of the test case contains one integer n — the length of a . The second line of the test case contains n integers (a_1), (a_2), ... (a_n) (1(leq) (a_i) (leq) 2 X(10^5) )。
输出描述
For each test case, print the answer: the length of the shortest prefix of elements you need to erase from aa to make it a good array.
思路:依据题意,构成序列C的大致模拟过程如下图: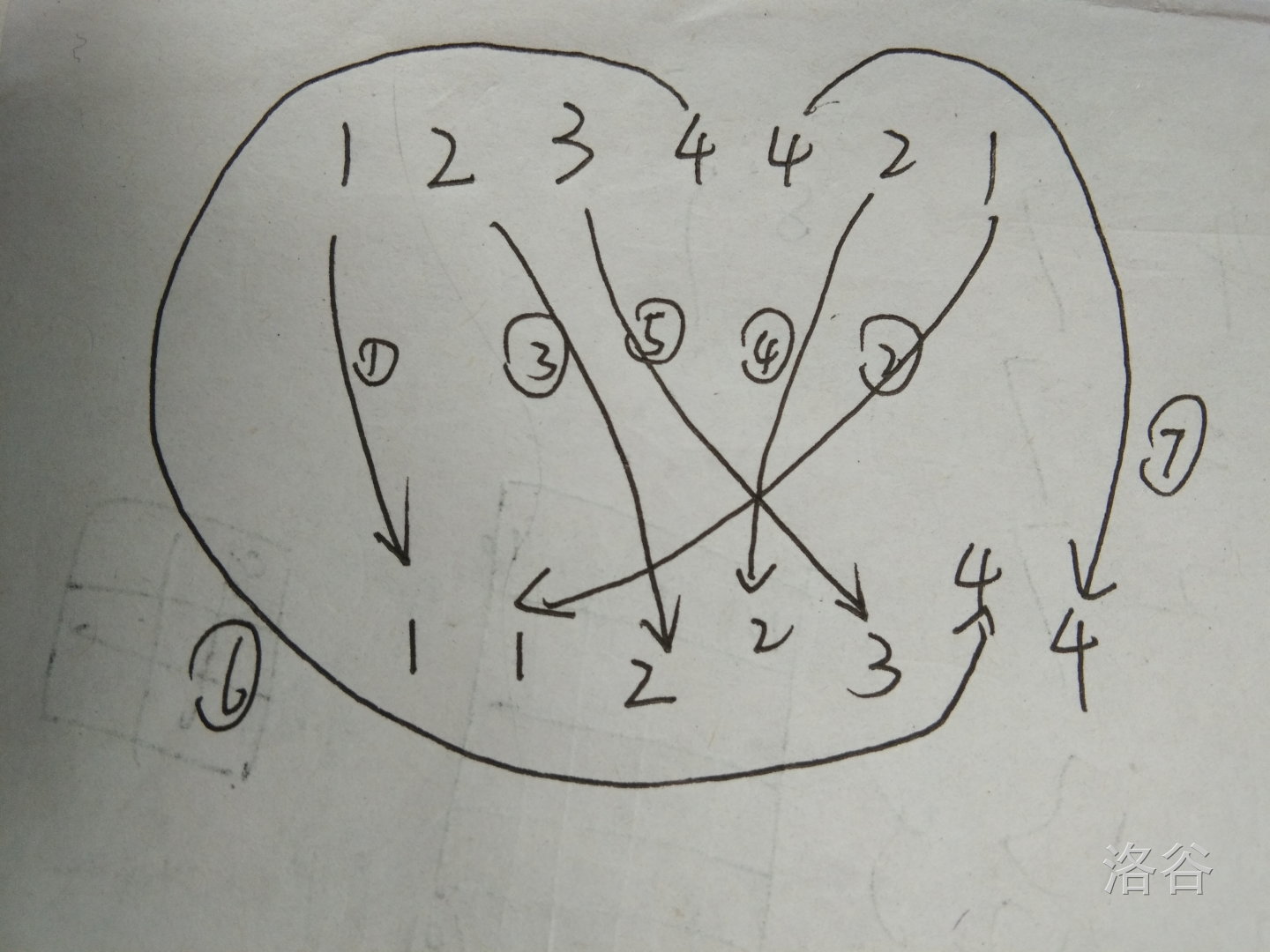
因此能够构成C单调不降的序列B应当满足1.单调不升(即a[i] (leq) a[i-1]) 2.单调不降(即a[i] (geq) a[i-1]) 3.两头大中间小 (eg: 1 2 2 3 5 4 1)。由于题目要求的是删除前缀,因此我们保留的是后缀。从序列的后缀中维护出一段满足题意的序列C就可以了。
参考代码如下:
#include<iostream>
#include<cstdio>
using namespace std;
int a[200005];
int main()
{
int t;
cin>>t;
while(t--)
{
int n;
scanf("%d",&n);
for(int i=1;i<=n;i++)
scanf("%d",&a[i]);
int k=n;
for(k=n-1;k>=1;k--)
{
if(a[k]<a[k+1])
break;
}
for(;k>=1;k--)
{
if(a[k]>a[k+1])
break;
}
cout<<k<<endl;
}
return 0;
}