一、简单定义
本质上仍然是一棵线段树,但它和普通线段树不同,其每个节点用来表示一个区间内元素出现的次数,可以理解为维护区间的值域。
二、应用
1.维护一段区间的数出现的次数,快速计算一段区间的数的出现次数。
2.快速找到第k大或第k小值。
缺点:只能离线操作,不能进行在线询问。
三、原理
例如,最初有一个序列 7 2 3 5 6 1 4,线段树初始状态各个结点的值都是0。如下图:
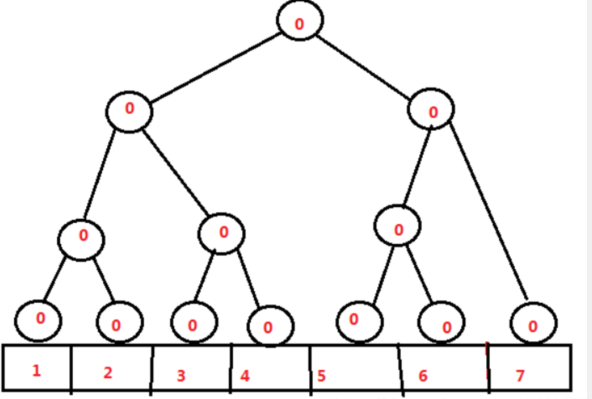
依次先插入7,线段树变为下图
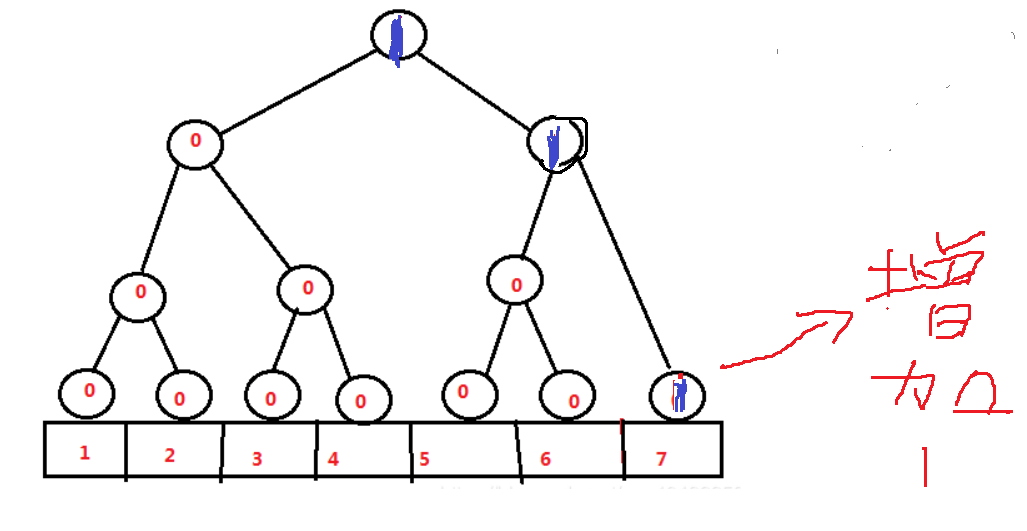
然后再插入元素2,此时根节点更新为2,根节点维护了1~7数字出现的个数,出现了一次7和一次2,总次数那自然是2了
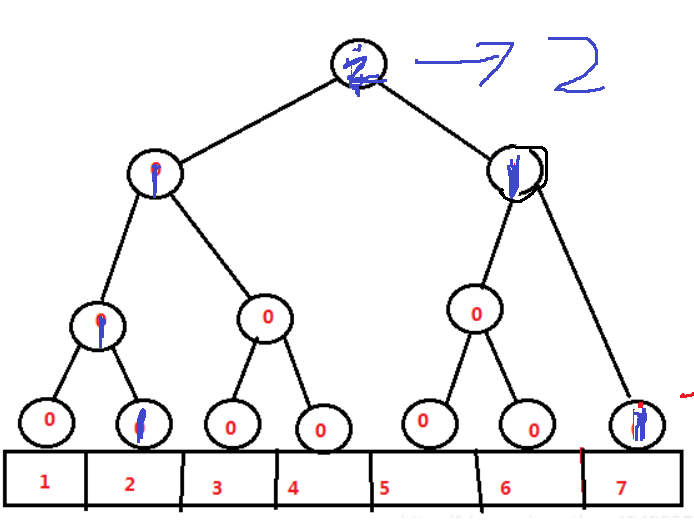
再插入元素3,同样地去递归更新结点,如下图所示

此时,当更新元素3的个数之前,我们可以查询[1,2]的权值和区间[4,7]的权值,可以得到比3小的元素有几个,比3大的元素有几个,那么可以轻易地得出当前出现的元素3是第k小和第k大
四、相关代码
1.单点更新。依然是递归到叶子节点p,令t[p]++

1 void upd(int l,int r,int x,int p){ 2 if(l==r) {t[p]++;return;} 3 int mid = (l+r)>>1; 4 if(x<=mid) upd(l,mid,x,p<<1); 5 else upd(mid+1,r,x,p<<1|1); 6 t[p] = t[p<<1]+t[p<<1|1]; 7 }
2.查询一段区间[l,r]数字出现的总和

1 int query(int ql,int qr,int l,int r,int p){ 2 if(l>=ql && r<=qr) return t[p]; 3 int mid = (l+r)>>1; 4 int ans = 0; 5 if(ql<=mid) ans+=query(ql,qr,l,mid,p<<1); 6 if(qr>mid) ans+=query(ql,qr,mid+1,r,p<<1|1); 7 return ans; 8 }
3.查询所有数中的第k大(第k小)

1 int kth(int l,int r,int k,int p) 2 { 3 if(l == r) return l; 4 else{ 5 int mid = l+r>>1; 6 int s1 = t[p<<1],s2 = t[p<<1|1]; 7 if(k<=s2) return kth(mid+1,r,p<<1|1,k); 8 else return kth(l,mid,p<<1,k - s2); 9 } 10 }
五、例题
以查询第k大为例,权值线段树的核心是到每个结点,如果右子树的权值总和大于了k,则说明其第k大值在右子树,递归进入右子树。反之则说明第k大值在左子树。
特别注意:若要进入左子树,需要k减去右子树的总和,比如要找的元素是第5大,右子树权值总和为3,则需5-3=2,说明该节点的第5大值存在于左子树的第2大值中。那么从左子树递归下去,直到递归到一个数,那就是答案了。
1.hdu1394 Minimum Inversion Number
http://acm.hdu.edu.cn/showproblem.php?pid=1394
在先询问逆序对个数的最小值。给定一个序列,每次把序列的第一个数移动到最后,求每次操作后新序列的逆序对个数的最小值。
首先元素的数据范围不大,不必离散化,直接开权值线段树,结点维护元素的个数。离线,每次输入一个数,查询操作求出比其大的数字的个数,然后做单点更新。
再for一遍序列,每次把元素a[i]移动到最后,新增的答案贡献等于ans先减去比a[i]小的元素(因为把a[i]要放置最后),再加上比a[i]大的元素,这样更新下去,取min即可。

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 1e4 + 5; 5 int t[maxn<<2]; 6 int a[maxn]; 7 int n; 8 void upd(int l,int r,int x,int p){ 9 if(l==r) {t[p]++;return;} 10 int mid = (l+r)>>1; 11 if(x<=mid) upd(l,mid,x,p<<1); 12 else upd(mid+1,r,x,p<<1|1); 13 t[p] = t[p<<1]+t[p<<1|1]; 14 } 15 int query(int ql,int qr,int l,int r,int p){ 16 if(l>=ql && r<=qr) return t[p]; 17 int mid = (l+r)>>1; 18 int ans = 0; 19 if(ql<=mid) ans+=query(ql,qr,l,mid,p<<1); 20 if(qr>mid) ans+=query(ql,qr,mid+1,r,p<<1|1); 21 return ans; 22 } 23 int main() { 24 while(~scanf("%d",&n)){ 25 memset(t,0,sizeof(t)); 26 int x,ans=0; 27 for(int i=1;i<=n;++i){ 28 scanf("%d",&a[i]); 29 ans+=query(a[i]+1,n,1,n,1); 30 // cout<<ans<<" "; 31 upd(1,n,a[i]+1,1); 32 }int res=ans; 33 for(int i=1;i<=n;++i){ 34 res-=query(1,a[i]+1,1,n,1)-1; 35 res+=query(a[i]+1,n,1,n,1)-1; 36 // cout<<res<<" "; 37 ans=min(ans,res); 38 }printf("%d ",ans); 39 } 40 return 0; 41 }
2.洛谷P1637 三元上升子序列
https://www.luogu.com.cn/problem/P1637
求ai<aj<ak的三元组个数
首先每个元素的数据范围很大在longlong范围内,需要离散化处理一下,否则线段树MLE。
开权值线段树,一遍从1到n遍历维护一个权值线段树,用来预处L[i](左边比ai小的元素个数)。一遍从n到1遍历维护一个权值线段树,预处理R[i](右边比ai大的元素的个数)。
最后再for一遍a数组,根据乘法原理对于ai其组成的三元组为R[i]*L[i],整体求出∑R[i]*L[i]即可。具体请看代码

1 #include<bits/stdc++.h> 2 using namespace std; 3 typedef long long ll; 4 const int maxn = 3e4 + 5; 5 int t[maxn<<2]; 6 ll a[maxn],tmp[maxn],L[maxn],R[maxn]; 7 int n; 8 void upd(int l,int r,int x,int p){ 9 if(l==r) {t[p]++;return;} 10 int mid = (l+r)>>1; 11 if(x<=mid) upd(l,mid,x,p<<1); 12 else upd(mid+1,r,x,p<<1|1); 13 t[p] = t[p<<1]+t[p<<1|1]; 14 } 15 int query(int ql,int qr,int l,int r,int p){ 16 if(l>=ql && r<=qr) return t[p]; 17 int mid = (l+r)>>1; 18 int ans = 0; 19 if(ql<=mid) ans+=query(ql,qr,l,mid,p<<1); 20 if(qr>mid) ans+=query(ql,qr,mid+1,r,p<<1|1); 21 return ans; 22 } 23 24 25 int main() { 26 scanf("%d",&n); 27 for(int i = 1;i<=n;i++){ 28 scanf("%d",&a[i]); 29 tmp[i] = a[i]; 30 } 31 sort(tmp+1,tmp+1+n); 32 int up = unique(tmp+1,tmp+1+n) - (tmp+1); 33 unordered_map<ll,int> m; 34 for(int i = 1;i<=up;i++) m[tmp[i]] = i; 35 36 for(int i = 1;i<=n;i++){ 37 int pos = m[a[i]];//离散化后的大小 38 if(pos!=1) L[i] = query(1,pos-1,1,up,1); 39 upd(1,up,pos,1); 40 } 41 memset(t,0,sizeof(t)); 42 for(int i = n;i>=1;i--){ 43 int pos = m[a[i]]; 44 if(pos!=up) R[i] = query(pos+1,up,1,up,1); 45 upd(1,up,pos,1); 46 } 47 ll ans = 0; 48 for(int i = 1;i<=n;i++){ 49 ans+=(L[i]*R[i]); 50 } 51 printf("%lld",ans); 52 return 0; 53 } 54 //
3.hdu4217 Data Structure?
http://acm.hdu.edu.cn/showproblem.php?pid=4217
每次查询第k小,从序列中拿出,求所有询问的总和。权值线段树的板子题,直接开权值线段树,每次查询第k小,随后单点更新删除即可。

1 #include<cstring> 2 #include<iostream> 3 #include<cstdio> 4 using namespace std; 5 typedef long long ll; 6 const int maxn = 265000; 7 int t[maxn<<2]; 8 int n; 9 void build(int l,int r,int p){ 10 if(l == r) {t[p] = 1;return;} 11 int mid = l+r>>1; 12 build(l,mid,p<<1); 13 build(mid+1,r,p<<1|1); 14 t[p] = t[p<<1] + t[p<<1|1]; 15 } 16 void upd(int l,int r,int x,int p,int v){ 17 if(l==r) {t[p]+=v;return;} 18 int mid = (l+r)>>1; 19 if(x<=mid) upd(l,mid,x,p<<1,v); 20 else upd(mid+1,r,x,p<<1|1,v); 21 t[p] = t[p<<1]+t[p<<1|1]; 22 } 23 int query(int ql,int qr,int l,int r,int p){ 24 if(l>=ql && r<=qr) return t[p]; 25 int mid = (l+r)>>1; 26 int ans = 0; 27 if(ql<=mid) ans+=query(ql,qr,l,mid,p<<1); 28 if(qr>mid) ans+=query(ql,qr,mid+1,r,p<<1|1); 29 return ans; 30 } 31 int findkth(int l,int r,int k,int p) 32 { 33 if(l == r) return l; 34 else{ 35 int mid = l+r>>1; 36 int s1 = t[p<<1],s2 = t[p<<1|1]; 37 if(k<=s1) return findkth(l,mid,k,p<<1); 38 else return findkth(mid+1,r,k - s1,p<<1|1); 39 } 40 } 41 int main() { 42 int T; 43 scanf("%d",&T); 44 int cnt = 1; 45 while(T--){ 46 int n,k; 47 scanf("%d%d",&n,&k);; 48 build(1,n,1); 49 ll sum = 0; 50 for(int i = 1;i<=k;i++){ 51 int kth; 52 scanf("%d",&kth); 53 int take = findkth(1,n,kth,1); 54 sum +=take; 55 upd(1,n,take,1,-1); 56 } 57 printf("Case %d: %lld ",cnt,sum); 58 cnt++; 59 } 60 return 0; 61 } 62 //
