一 前言
前面的文章已经介绍了五种不同的分类器,它们各有优缺点。我们可以很自然地将不同的分类器组合起来,而这种组合结果则被成为集成方法(ensemble method)或者元算法(meta-algorithm)。使用集成方法时会有多种形式:可以是不同算法的集成,也可以是同一种算法在不同设置下的集成,还可以是数据集不同部分分配给不同分类器之后的集成。
二 集成方法
集成方法(ensemble method)通过组合多个基分类器(base classifier)来完成学习任务,颇有点“三个臭皮匠顶个诸葛亮”的意味。基分类器一般采用的是弱可学习(weakly learnable)分类器,通过集成方法,组合成一个强可学习(strongly learnable)分类器。所谓弱可学习,是指学习的正确率仅略优于随机猜测的多项式学习算法;强可学习指正确率较高的多项式学习算法。集成学习的泛化能力一般比单一的基分类器要好,这是因为大部分基分类器都分类错误的概率远低于单一基分类器的。
集成方法主要包括Bagging和Boosting两种方法,Bagging和Boosting都是将已有的分类或回归算法通过一定方式组合起来,形成一个性能更加强大的分类器,更准确的说这是一种分类算法的组装方法,即将弱分类器组装成强分类器的方法。
1 Bagging
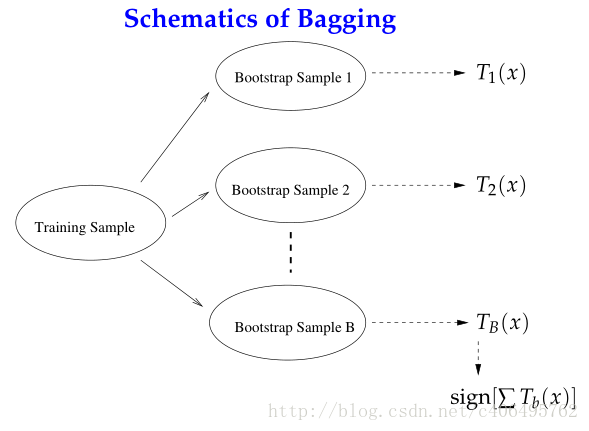
自举汇聚法(bootstrap aggregating),也称为bagging方法。Bagging对训练数据采用自举采样(boostrap sampling),即有放回地采样数据,主要思想:
- 从原始样本集中抽取训练集。每轮从原始样本集中使用Bootstraping的方法抽取n个训练样本(在训练集中,有些样本可能被多次抽取到,而有些样本可能一次都没有被抽中)。共进行k轮抽取,得到k个训练集。(k个训练集之间是相互独立的)
- 每次使用一个训练集得到一个模型,k个训练集共得到k个模型。(注:这里并没有具体的分类算法或回归方法,我们可以根据具体问题采用不同的分类或回归方法,如决策树、感知器等)
- 对分类问题:将上步得到的k个模型采用投票的方式得到分类结果;对回归问题,计算上述模型的均值作为最后的结果。(所有模型的重要性相同)
2 Boosting
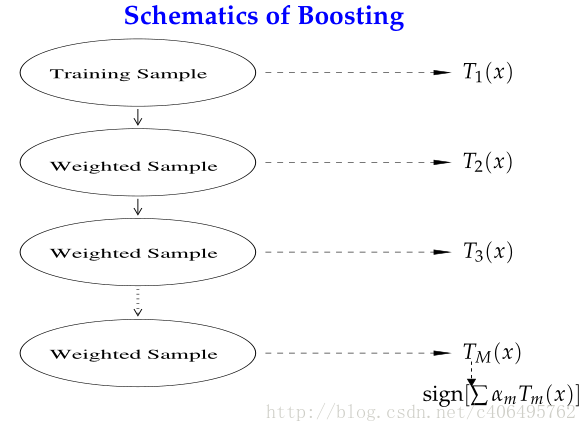
Boosting是一种与Bagging很类似的技术。Boosting的思路则是采用重赋权(re-weighting)法迭代地训练基分类器,主要思想:
- 每一轮的训练数据样本赋予一个权重,并且每一轮样本的权值分布依赖上一轮的分类结果。
- 基分类器之间采用序列式的线性加权方式进行组合。
三 Bagging、Boosting二者之间的区别
样本选择上:
- Bagging:训练集是在原始集中有放回选取的,从原始集中选出的各轮训练集之间是独立的。
- Boosting:每一轮的训练集不变,只是训练集中每个样例在分类器中的权重发生变化。而权值是根据上一轮的分类结果进行调整。
样例权重:
- Bagging:使用均匀取样,每个样例的权重相等。
- Boosting:根据错误率不断调整样例的权值,错误率越大则权重越大。
预测函数:
- Bagging:所有预测函数的权重相等。
- Boosting:每个弱分类器都有相应的权重,对于分类误差小的分类器会有更大的权重。
并行计算:
- Bagging:各个预测函数可以并行生成。
- Boosting:各个预测函数只能顺序生成,因为后一个模型参数需要前一轮模型的结果。
四 总结
这两种方法都是把若干个分类器整合为一个分类器的方法,只是整合的方式不一样,最终得到不一样的效果,将不同的分类算法套入到此类算法框架中一定程度上会提高了原单一分类器的分类效果,但是也增大了计算量。
下面是将决策树与这些算法框架进行结合所得到的新的算法:
- Bagging + 决策树 = 随机森林
- AdaBoost + 决策树 = 提升树
- Gradient Boosting + 决策树 = GBDT
集成方法众多,本文主要关注Boosting方法中的一种最流行的版本,即AdaBoost。
代码如下: