求解非线性优化问题的有效手段
牛顿法:优点:收敛速度快 缺点:定步长迭代,有时会使函数值上升。计算量大,要求函数必须有连续的一、二阶偏导数,海森矩阵必须正定
拟牛顿法:在牛顿法的基础上加入了寻求最优步长因子
示例代码:求解目标函数的局部最小值
主函数:
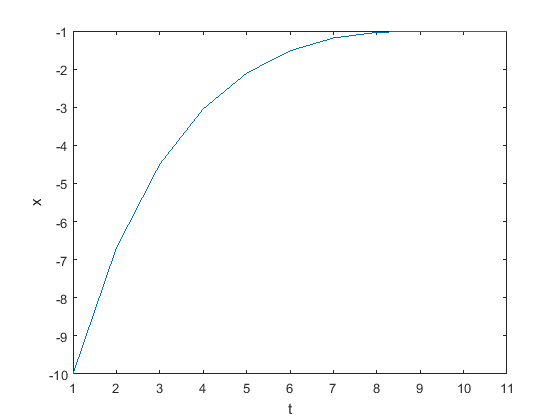
% Newton法求解目标函数的局部最小值 % Meringue % 2018/5/13 % --------------------------- clc; clear; % 迭代参数 x0 = -10; % 初始值 err0 = inf; % 误差初始设为inf iter = 0;% 迭代次数 errMax = 1e-3; % 最大容许误差 iterMax = 100; % 最大迭代次数 % 迭代过程 x(iter+1) = x0; while err0>errMax % 迭代终止条件1:达到最大迭代次数 if iter == iterMax disp('达到最大迭代次数!'); break; end % Newton迭代过程 iter = iter+1; [~,dy,d2y] = func1(x(iter)); x(iter+1) = x(iter)-dy/d2y; % 迭代终止条件2:找到满足精度要求的解 if abs(x(iter+1)-x(iter))<errMax disp('找到满足精度要求的解!') disp(['x = ',num2str(x(iter+1))]); disp(['迭代次数为',num2str(iter-1)]); break; end end % 迭代结果展示 plot(x) xlabel('t');ylabel('x')
目标函数:
%目标函数 function [y,dy,d2y] = func1(x) % y = x.^2-2 y = x.^4-2*x^2+1; dy = 4*x^3-4*x; d2y = 12*x^2-4;
运行结果: