ARC117F Gateau

Description

\(\mathcal{P}\text{ortal.}\)

题意简述：有一个长为 \(2n\) 的环形数组 \(A\)，全为自然数。给出 \(2n\) 条约束，约束 \(i\) 形如：从 \(i\) 开始的半环的和 \(\geqslant B_i\)。在满足所有约束的情况下，最小化 \(\sum A\) 的值，回答这个最小值。

Solution

一些闲话：本来是打算写在专题练习里面的，但后来写这题的代码时调整了很多次思路，也重构了很多次代码才终于过掉。发现自己的实现能力，一些 \(\text{corner cases}\) 的考虑都还有欠缺，所以专门开了一篇博客来记录这道题。不管怎么样，还是挺开心的 。

---

直接构造是不易的，所以考虑直接二分 \(M=\sum A\).

考虑破环为链，将区间值简单表示 —— 记 \(A\) 的前缀和为 \(S\)，考虑差分约束，那么 \(S\) 需要满足：

• \(S_{i-1}\leqslant S_i\)；

• \(S_0=0,S_{2n}\geqslant M\)，即 \(S_{2n}-S_0\geqslant M\)；

• \(\forall i\in [1,n+1],S_{i+n-1}-S_{i-1}\geqslant B_i\)；

• 现在还剩下 \(i\in (n+1,2n]\) 的区间限制没有描述，然而我们发现由于循环结构，它被断成了两个区间，那么这个不等式涉及的变量就很多了。怎么办呢？不妨直接令 \(S_{2n}-S_0=M\)（即再加上限制 \(S_{2n}-S_0\leqslant M\)），我们就可以用两个区间中间夹的区间来描述这条限制了，也就是 \(\forall i\in (n+1,2n],M-(S_{i-1}-S_{i-n+1})\geqslant B_i\).

但是用 \(\rm spfa\) 判断负环是 \(\mathcal O(n^2)\) 的，妥妥地 \(\mathtt{TLE}\) 掉。仔细观察这张图，实际上它是很有规律的：

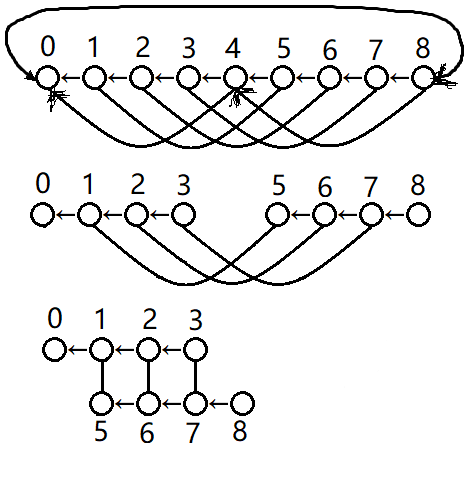
可以发现扔掉点 \(n\) 及其连接的边，和 \(2n\rightarrow 0,0\rightarrow 2n\) 的边，原图就变成了一张 \(\rm dag\)，可以直接在上面 \(\mathtt{dp}\) 求解最短路。求解之后将 \(n\) 加回去，此时只需要计算 与新加边有关 的点，整张图就缩成了 \(0,n-1,n,n+1,2n\) 五个点，再跑 \(\rm spfa\) 判负环即可。时间复杂度只有 \(\mathcal O(n\log V)\).

一个特别需要注意的代码细节是，形如上图的 \((1,5)\) 之间的边也可能形成负环，需要特别判断。这个锅不知道调了多久。

Code

# include <cstdio>
# include <cctype>
# define print(x,y) write(x), putchar(y)

template <class T>
inline T read(const T sample) {
    T x=0; char s; bool f=0;
    while(!isdigit(s=getchar())) f|=(s=='-');
    for(; isdigit(s); s=getchar()) x=(x<<1)+(x<<3)+(s^48);
    return f? -x: x;
}
template <class T>
inline void write(T x) {
    static int writ[50], w_tp=0;
    if(x<0) putchar('-'), x=-x;
    do writ[++w_tp]=x-x/10*10, x/=10; while(x);
    while(putchar(writ[w_tp--]^48), w_tp);
}

# include <queue>
# include <vector>
# include <iostream>
using namespace std;
typedef long long _long;
typedef pair <int,_long> par;

const int maxn = 300005;
const _long infty = 1e17;

bool inq[maxn]; _long dp[maxn];
int n, b[maxn], m, upd[maxn];
vector <par> e[maxn];

bool spfa() {
    queue <int> q; q.push(m), dp[m]=0;
    dp[n+1]=dp[n]=dp[n-1]=dp[0]=infty;
    upd[n+1]=upd[n]=upd[n-1]=upd[0]=upd[m]=0;
    inq[n+1]=inq[n]=inq[n-1]=inq[0]=0, inq[m]=1;
    while(!q.empty()) {
        int u = q.front(); q.pop(); inq[u]=0;
        for(const auto& t:e[u]) {
            int v=t.first; _long w=t.second;
            if(dp[v]>dp[u]+w) {
                upd[v] = upd[u]+1, dp[v]=dp[u]+w;
                if(upd[v]==5) return false;
                if(!inq[v]) q.push(v), inq[v]=1;
            }
        }
    } 
	return true;
}

void link(int x,int y,const _long& w) {
    e[x].emplace_back(make_pair(y,w));
}

void dpLast(const _long& mid) {
    dp[m-1]=dp[m]=0, dp[n-1]=-b[n];
    for(int i=n-2; i>=1; --i) {
        dp[i]=dp[i+1], dp[i+n]=dp[i+n+1];
        _long tmp1=dp[i], tmp2=dp[i+n];
        dp[i] = min(dp[i], tmp2-b[i+1]);
        dp[i+n] = min(dp[i+n], tmp1+mid-b[i+n+1]);
    } dp[0]=dp[1]; link(m,0,dp[0]);
    link(m,n+1,dp[n+1]), link(m,n-1,dp[n-1]);
}

void dpMiddle(const _long& mid) {
    dp[n-1]=0, dp[m-1]=mid-b[m];
    for(int i=n-2; i>=1; --i) {
        dp[i]=dp[i+1], dp[i+n]=dp[i+n+1];
        _long tmp1=dp[i], tmp2=dp[i+n];
        dp[i] = min(dp[i], tmp2-b[i+1]);
        dp[i+n] = min(dp[i+n], tmp1+mid-b[i+n+1]);
    } dp[0]=dp[1]; 
    link(n-1,n+1,dp[n+1]), link(n-1,0,dp[0]);
}

bool haveCircle(const _long& mid) {
	for(int i=1;i<n;++i) if(mid-b[i+1]-b[i+n+1]<0) 
		return true; return false;
}

bool judge(const _long& mid) {
	if(haveCircle(mid)) return false;
    e[0].clear();
    e[m].clear(), e[n+1].clear(),
    e[n-1].clear(), e[n].clear();
    dpLast(mid), dpMiddle(mid);
    link(m,0,-mid), link(n+1,n,0), link(n,n-1,0);
    link(m,n,-b[n+1]), link(n,0,-b[1]), link(0,m,mid);
    return spfa();
}

int main() {
    n=read(9); m = n<<1;
    for(int i=1;i<=m;++i) b[i]=read(9);
	if(n==1) return print(b[1]+b[2],'\n'), (0-0);
    _long l=0, r=1e14, mid, ans=-1;
    while(l<r) {
        mid = l+r>>1;
        if(judge(mid)) ans=r=mid;
        else l=mid+1;
    } print(ans,'\n');
    return 0;
}