[Contest on 2022.6.20] (👉ﾟヮﾟ)👉👈(●ˇ∀ˇ●)👉👈(ﾟヮﾟ👈)

\(\cal T_1\) 益智游戏

Description

一个 \(n × n\) 棋盘的每个格子被继续划分为了一个 \(2 × 2\) 的小棋盘，每个小棋盘中放了一个 \(1 × 2\) 的多米诺骨牌。

每个小棋盘有个修改代价，你需要花费最小的修改代价使得所有填了多米诺骨牌的小格子中心之间的距离不为 \(\sqrt 2\).

\(1 \leqslant n \leqslant 2000\).

多米诺骨牌从左到右编号为 \(1,2,3,4\):.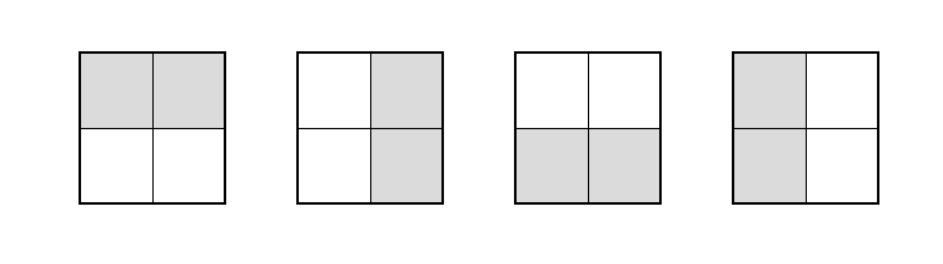

Solution

先考虑只有 \(1,2\) 骨牌的情况，容易发现一定是骨牌 \(1\) 为一段前缀，骨牌 \(2\) 为一段后缀，且随着行数增加，前缀长度不增。这个图形可以 \(\mathtt{dp}\)：设 \(dp(i,j)\) 为前 \(i\) 行，第 \(i\) 行分界线在 \(j\) 处的最小代价即可做到 \(\mathcal O(n^2)\).

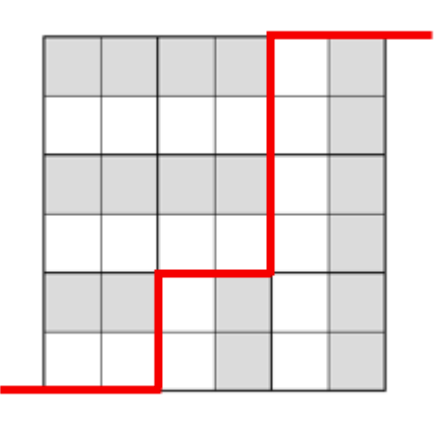
考虑所有骨牌，每一行从左到右一定是先骨牌 \(4\)，后面跟一段骨牌 \(1\) 或 骨牌 \(3\)，最后一段骨牌 \(2\)。同样地，我们可以从四个方向来看这个图形，都遵循上述规律，所以它最后会长成这样的形态：

解释一下，由于每一列从上到下一定是先骨牌 \(1\)，后面跟一段骨牌 \(2\) 或 骨牌 \(4\)，最后一段骨牌 \(3\)，所以对于所有行而言，一定是先 \(4\rightarrow 1\rightarrow 2\)，再 \(4\rightarrow 3\rightarrow 2\)，于是可以将图形划分为两个部分，每个部分只有三种骨牌。更进一步，以 \(4\rightarrow 1\rightarrow 2\) 为例，由于骨牌 \(1\) 不能在任何除了骨牌 \(1\) 的骨牌类型下面。嗯，这个表述也是极具现实意义的。

所以假设第 \(i\) 行骨牌 \(1\) 的区间范围为 \([l_i,r_i]\)，那么下一行的区间范围一定有 \(l_{i+1}\geqslant l_i,r_{i+1}\leqslant r_i\)，我们惊喜地发现，如果以 \(4\rightarrow 1\rightarrow 2\) 类型最后一行的骨牌 \(1\) 区间 \([L,R]\) 中任意一个位置纵向划分，这个类型就可以规约到上述两种骨牌的情况，可以使用 \(\mathcal O(n^2)\) 的 \(\mathtt{dp}\) 解决。最后把四种类型拼起来即可。

另外还要注意的是，在上下拼接的时候骨牌 \(2,4\) 不能在同一列。

再详细地讲一下 \(\mathtt{dp}\)，对于左上角的部分是设 \(dp(i,j)\) 为填左上角 \(i\) 行 \(j\) 列的格子，且符合要求的最小修改代价，转移加入一行或一列。

Code

# include <cstdio>
# include <cctype>
# define print(x,y) write(x), putchar(y)

template <class T>
inline T read(const T sample) {
    T x=0; char s; bool f=0;
    while(!isdigit(s=getchar())) f|=(s=='-');
    for(; isdigit(s); s=getchar()) x=(x<<1)+(x<<3)+(s^48);
    return f? -x: x;
}
template <class T>
inline void write(T x) {
    static int writ[50], w_tp=0;
    if(x<0) putchar('-'), x=-x;
    do writ[++w_tp]=x-x/10*10, x/=10; while(x);
    while(putchar(writ[w_tp--]^48), w_tp);
}

# include <cstring>
# include <iostream>
using namespace std;

# define int long long

const int maxn = 2005;

int n, c[maxn][maxn], a[maxn][maxn];
int dp[4][maxn][maxn], f[4][maxn][maxn];

int val(int x,int y,int v) {
    return a[x][y]==v? 0: c[x][y];
}

signed main() {
    freopen("game.in","r",stdin);
    freopen("game.out","w",stdout);
    n=read(9);
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j) a[i][j]=read(9);
    for(int i=1;i<=n;++i)
        for(int j=1;j<=n;++j) c[i][j]=read(9);
    int ans = 1e18;
    for(int i=1;i<=n;++i) for(int j=1;j<=n;++j)
        f[0][i][j] = f[0][i-1][j]+val(i,j,1),
        f[3][i][j] = f[3][i][j-1]+val(i,j,4);
    for(int i=n;i;--i) for(int j=n;j;--j)
        f[1][i][j] = f[1][i][j+1]+val(i,j,2),
        f[2][i][j] = f[2][i+1][j]+val(i,j,3);
    for(int i=1;i<=n;++i) for(int j=1;j<=n;++j)
        dp[0][i][j] = min(dp[0][i-1][j]+f[3][i][j],dp[0][i][j-1]+f[0][i][j]);
    for(int i=1;i<=n;++i) for(int j=n;j;--j)
        dp[1][i][j] = min(dp[1][i-1][j]+f[1][i][j],dp[1][i][j+1]+f[0][i][j]);
    for(int i=n;i;--i) for(int j=1;j<=n;++j)
        dp[2][i][j] = min(dp[2][i+1][j]+f[3][i][j],dp[2][i][j-1]+f[2][i][j]);
    for(int i=n;i;--i) for(int j=n;j;--j)
        dp[3][i][j] = min(dp[3][i+1][j]+f[1][i][j],dp[3][i][j+1]+f[2][i][j]);
    for(int i=0;i<=n;++i) for(int j=0;j<=n;++j)
        ans = min(ans, dp[0][i][j]+dp[1][i][j+1]+dp[2][i+1][j]+dp[3][i+1][j+1]);
    print(ans,'\n');
    return 0;   
}

\(\cal T_2\) 华为

Description

有两个变量 \(x, y\)，初始有 \(x ← 0,y ← 0\)。每个时刻唐芯会选择恰好一个变量令其加 \(1\)，更具体地，有 \(p\) 的概率令 \(x ← x + 1\)，\(q\) 的概率令 \(y ← y + 1\)，且有 \(p + q = 1\).

你需要对 \(t\) 组 \(X_i , Y_i\)，求第一次满足 \(x ≡ X_i \pmod n\) 且 \(y ≡ Y_i \pmod m\) 的期望时 间。

为了避免精度误差，答案对 \(998244353\) 取模。

\(2\leqslant n,m\)，\(n\leqslant 10^9,m\leqslant 400,t\leqslant 500\).

Solution

一些闲话：今天的题目是多项式专场吗？可是我多项式烂得不行欸 。

首先可以设 \(dp(i,j)\) 为从 \(x=i,y=j\) 开始，第一次满足 \(x ≡ X_i \pmod n\) 且 \(y ≡ Y_i \pmod m\) 的期望时间，转移就有

\[dp(i,j)=p\cdot dp((i+1)\bmod n,j)+q\cdot dp(i,(j+1)\bmod m)+1 \]

事实上，可以发现从 \((X_i,Y_i)\) 到达 \((0,0)\) 和从 \((-X_i,-Y_i)\) 到达 \((0,0)\) 是等价的，于是改写一下这个转移

\[dp(i,j)=p\cdot dp((i-1+n)\bmod n,j)+q\cdot dp(i,(j-1+m)\bmod m)+1 \]

再将 \((-X_i,-Y_i)\) 平移到 \((0,0)\)，这样数组下标就又变成了正数。这个形式便于之后的操作。

第一维的数字范围达到了惊人的 \(10^9\) 级别，不妨考虑一下 \(\log\) 级的算法，为了方便，将与 \(dp(i,j)\) 同一行的元素展开（因为第二维处在模意义下，所以转大概 \(m\) 次就能转回 \(dp(i,j)\)），这样就可以直接用上一行的元素进行递推

\[(1-q^m)\cdot dp(i,j)=\frac{1-q^m}{1-q}+p\cdot \sum_{k=0}^{m-1}q^k\cdot dp((i-1+n)\bmod n,j) \]

也就是

\[dp(i,j)=\frac{1}{1-q}+\sum_{k=0}^{m-1}\frac{pq^k}{1-q^m}\cdot dp((i-1+n)\bmod n,(j-k+m)\bmod m) \]

发现 \(\dfrac{pq^k}{1-q^m}\) 和 \(j\) 无关，只和 \(k\) 有关，事实上，这就是一个 循环卷积 的形式，所以可以令 \(f_k=\sum_{i=0}^{m-1}dp(k,i)\cdot x^i,\ g=\sum_{i=0}^{m-1}\frac{pq^i}{1-q^m}\cdot x^i,\ h=\sum_{i=0}^{m-1}\frac{1}{1-q}\cdot x^i\)，那么有

\[f_k=f_{k-1}*g+h \]

由于循环卷积有结合律，所以可以预处理出 \(g\) 的 \(2\) 的幂次再卷积，成功将卷积次数从 \(\mathcal O(n)\) 降低到 \(\mathcal O(\log n)\) 级别。对于 \(h\)，由于其结构比较简单，所以可以直接手算结果（小提示：\(h\) 不管卷上 \(g\) 几次所有位置的系数都是一样的哟）。

时间复杂度 \(\mathcal O(m^3+tm\log m\log V)\).

Code

# pragma GCC optimize("Ofast")
# pragma GCC optimize("inline")

# include <cstdio>
# include <cctype>
# define print(x,y) write(x), putchar(y)

template <class T>
inline T read(const T sample) {
    T x=0; char s; bool f=0;
    while(!isdigit(s=getchar())) f|=(s=='-');
    for(; isdigit(s); s=getchar()) x=(x<<1)+(x<<3)+(s^48);
    return f? -x: x;
}
template <class T>
inline void write(T x) {
    static int writ[50], w_tp=0;
    if(x<0) putchar('-'), x=-x;
    do writ[++w_tp]=x-x/10*10, x/=10; while(x);
    while(putchar(writ[w_tp--]^48), w_tp);
}

# include <cstring>
# include <iostream>
using namespace std;
typedef long long _long;

const int maxn = 405;
const int saiz = 2000;
const int mod = 998244353, G = 3;

int inv(int x,int y=mod-2,int r=1) {
    for(; y; y>>=1, x=1ll*x*x%mod)
        if(y&1) r=1ll*r*x%mod; return r;
} const int iG = inv(G);

int n, m, rev[saiz], lim=1, _inv, bit, mom, fir;
_long _p, _q, a[405][405], f[30][saiz], g[saiz], h[saiz];

void gauss(int n) {
    int j, tmp, Inv;
    for(int i=0;i<n;++i) {
        for(j=i; j<n && !a[j][i]; ++j);
        if(i^j) swap(a[i],a[j]);
        Inv = inv(a[i][i]);
        for(j=i+1; j<n; ++j) if(a[j][i]) {
            int tmp = a[j][i]*Inv%mod;
            for(int k=i; k<=n; ++k)
                a[j][k] = (a[j][k]-a[i][k]*tmp)%mod;
        }
    }
    for(int i=n-1; i>=0; --i) {
        for(int j=i+1; j<n; ++j)
            a[i][n] = (a[i][n]-a[j][j]*a[i][j])%mod;
        a[i][i] = a[i][n]*inv(a[i][i])%mod;
    }
}

void ntt(_long* f,bool opt=0) {
    for(int i=0;i<lim;++i) 
        if(i<rev[i]) swap(f[i],f[rev[i]]);
    for(int mid=1; mid<lim; mid<<=1) {
        int wn = inv(opt? iG: G, (mod-1)/(mid<<1));
        for(int i=0; i<lim; i+=(mid<<1)) {
            int w = 1;
            for(int j=0; j<mid; ++j, w=1ll*w*wn%mod) {
                _long tmp = f[i|j|mid]*w;
                f[i|j|mid] = (f[i|j]-tmp)%mod,
                f[i|j] = (f[i|j]+tmp)%mod;
            }
        }
    } if(!opt) return; 
    for(int i=0;i<lim;++i) f[i] = f[i]*_inv%mod;
}

int calc(int n) {
    static const int coe = inv(_p);
    if(!n) return 0;
    return 1ll*coe*n%mod;
}

int main() {
    freopen("huawei.in","r",stdin);
    freopen("huawei.out","w",stdout);
    n=read(9), m=read(9), _p=read(9), _q=read(9);
    mom = inv(_p+_q); _p=1ll*_p*mom%mod, _q=1ll*_q*mom%mod;
    mom = inv((mod+1-inv(_q,m))%mod);
    while(lim<m+m-1) lim<<=1, ++bit; _inv=inv(lim);
    for(int i=0;i<lim;++i) 
        rev[i] = (rev[i>>1]>>1)|((i&1)<<bit-1);
    for(int i=0;i<m;++i) 
        f[0][i] = 1ll*_p*inv(_q,i)%mod*mom%mod;
    for(int i=1;i<30;++i) {
        memcpy(g,f[i-1],sizeof(_long)*m);
        memset(g+m,0,sizeof(_long)*(lim-m));
        ntt(g); for(int j=0;j<lim;++j) g[j]=g[j]*g[j]%mod; ntt(g,1); 
        for(int j=0;j<lim;++j) f[i][j%m] = (f[i][j%m]+g[j])%mod;
    } h[0]=1;
    for(int i=0;i<30;++i) if((n-1)>>i&1) {
        memcpy(g,f[i],sizeof(_long)*m);
        memset(g+m,0,sizeof(_long)*(lim-m));
        ntt(g), ntt(h);
        for(int j=0;j<lim;++j) 
            g[j] = g[j]*h[j]%mod, h[j]=0;
        ntt(g,1);
        for(int j=0;j<lim;++j) h[j%m] = (h[j%m]+g[j])%mod;
    } a[0][0]=1;
    int jinx = 1ll*calc(n-1)*_p%mod;
    for(int i=1;i<m;++i) {
        a[i][m]=a[i][i]=1, a[i][i-1]=-_q;
        for(int j=0;j<m;++j)
            a[i][j] = (a[i][j]-h[(i-j+m)%m]*_p%mod)%mod;
        a[i][m] = (a[i][m]+jinx)%mod;
    } gauss(m);
    for(int T=read(9); T; --T) {
        int x=read(9), y=read(9);
        for(int i=0;i<m;++i) h[i]=a[i][i];
        for(int i=m;i<lim;++i) h[i]=0;
        for(int i=0;i<30;++i) if(x>>i&1) {
            memcpy(g,f[i],sizeof(_long)*m);
            memset(g+m,0,sizeof(_long)*(lim-m));
            ntt(h), ntt(g);
            for(int j=0;j<lim;++j) 
                g[j] = g[j]*h[j]%mod, h[j]=0;
            ntt(g,1);
            for(int j=0;j<lim;++j) h[j%m] = (h[j%m]+g[j])%mod;
        } print(((h[y]+calc(x))%mod+mod)%mod,'\n'); 
    }
    return 0;
}

\(\cal T_3\) 区间距离

Description

唐芯有两个长度为 \(n\) 的序列 \(a_1, a_2, \dots , a_n\) 和 \(b_1, b_2, \dots , b_n\)，你需要支持 \(q\) 次询问，每次询问给定 \((p_1, p_2, x)\)，你需要回答下式的值

\[\sum^x_{i=1} |a_{p_1+i-1} − b_{p_2+i−1}| \]

因为一些原因，\(a, b\) 的值都非常小。

\(1\leqslant n\leqslant 10^5,1\leqslant q\leqslant 10^6,1\leqslant a_i,b_i\leqslant 5\).

Solution

Method 1: \(\rm bitset\)

这么明显的枚举权值，我竟然没想到 。

枚举 \(c=2,3,4,5\)，将每个位置上的权值赋为 \([a_i\geqslant c]\)，那么绝对值就转化成了异或后的 \(\text{popcount}\)。考虑分块，记块长为 \(\omega\)，将 \(n\) 扩张到 \(\max \{m\omega\},\text{s.t. }(m-1)\omega<n\)。对于询问 \((x,y,L)\)，考虑 \(x\) 到 \(y\) 的偏移量 \(d=(y-x+m\omega)\bmod m\omega\)，再对 \(d\bmod \omega\) 的结果进行分类。

对于每一种 \(r\in [0,\omega)\)，对应的 \(\{a\}\) 就是 \(m\) 个大小为 \(\omega\) 的块，\(\{b\}\) 就是前面一段长度为 \(r\) 的区间，再加上 \(m\) 个大小为 \(\omega\) 的块。可以发现 \(\{a\},\{b\}\) 的块进行匹配的不同实际上只由 \(\{a\}\) 的第一块和 \(\{b\}\) 中的第 \(i\in [1,m]\) 块进行匹配决定，所以情况数只有 \(n/\omega\) 种。另外，对于每一种情况，我们需要以 \(\mathcal O(n/\omega)\) 的复杂度来计算块与块匹配的答案（不妨设 \(\omega=64\)，用 unsigned long long 进行存储），所以复杂度是 \(\mathcal O(\max c\cdot \omega\cdot (n/\omega)\cdot (n/\omega))=\mathcal O(\max c\cdot n^2/\omega)\).

另外讲一下如何计算询问的答案。将询问分到对应的 \(r\) 中，分到对应的 \(\{a\}\) 中第一块匹配了什么。然后对于被分到同一组的询问，可以差分求解。

最后处理散块的情况，是 \(\mathcal O(q\omega)\) 的。我觉得真不好写，代码能力真的好弱。

Method 2: 分块 + \(\mathtt{FFT}\)

说个笑话：我今天才知道字符串通配符匹配问题可以用 \(\mathtt{FFT}\) 解决 。

还是定义字符串的匹配函数 \(\text{match}(x,y)=a_x\oplus b_y=(a_x-b_y)^2\)，那么不妨先假设 \(\{a\}\) 的第零位与 \(\{b\}\) 中从 \(x\) 开始的字符串的匹配贡献为（假设匹配长度为 \(m\)）

\[P(x)=\sum_{i=0}^{m-1}\text{match}(i,x+i) \]

暴力展开柿子就有

\[P(x)=\sum_{i=0}^{m-1}a_i^2 +\sum_{i=0}^{m-1} b_{x+i}^2-2\cdot \sum_{i=0}^{m-1}a_i\cdot b_{x+i} \]

前面两坨都可以快速求得，考虑最后一坨怎么计算，容易想到将 \(\{a\}\) 前面长度为 \(m\) 的部分翻转，就变成了卷积的形式，可以在 \(\mathcal O((n+m)\log (n+m))\) 的时间中求得。另外可以发现，我们并不需要对每个 \(x\) 都卷一次，只需要将长度为 \(m\) 的 \(\{a\}\) 和长度为 \(n\) 的 \(\{b\}\) 卷起来即可。

现在考虑如何将上文的方法迁移到本题。由于 \(\{a\}\) 的开始匹配位是每次询问重新给定的，所以考虑分块 —— 具体地，对于每一块的开头都对应一个 \(P(x)\) 即可。

Code

只写了第一种方法。

# pragma GCC optimize("Ofast")
# pragma GCC optimize("inline")

# include <cstdio>
# include <cctype>
# define print(x,y) write(x), putchar(y)

template <class T>
inline T read(const T sample) {
    T x=0; char s; bool f=0;
    while(!isdigit(s=getchar())) f|=(s=='-');
    for(; isdigit(s); s=getchar()) x=(x<<1)+(x<<3)+(s^48);
    return f? -x: x;
}
template <class T>
inline void write(T x) {
    static int writ[50], w_tp=0;
    if(x<0) putchar('-'), x=-x;
    do writ[++w_tp]=x-x/10*10, x/=10; while(x);
    while(putchar(writ[w_tp--]^48), w_tp);
}

# include <vector>
# include <iostream>
# include <algorithm>
using namespace std;
typedef unsigned long long uns;

const int w = 64;
const int maxb = 1600;
const int maxn = 1e5+5;
const int maxm = 1e6+5;

uns a[maxb], b[maxb];
int n, q, A[maxn], B[maxn], ans[maxm], bl[maxn];
struct node { int p1,p2,L,id; };
struct Node { int pos,coe,id; };
vector <node> vec[67];
vector <Node> rec[maxb];

int Abs(int x) { return x>0?x:-x; }

int main() {
    freopen("dist.in","r",stdin);
    freopen("dist.out","w",stdout);
    n=read(9), q=read(9); int m = (n-1)/w+1, lim=m*w;
    for(int i=1;i<=n;++i) A[i]=read(9);
    for(int i=1;i<=n;++i) B[i]=read(9);
    for(int i=1;i<=q;++i) {
        int x=read(9), y=read(9), L=read(9);
        vec[((y-x+lim)%lim)%w].emplace_back((node){x,y,L,i});
    }
    for(int i=1;i<=n;++i) bl[i] = (i-1)/w+1;
    for(int c=2;c<=5;++c) {
        for(int i=1;i<=m;++i) {
            int R=min(i*w,n), L=(i-1)*w+1; a[i]=0;
            for(int j=L; j<=R; ++j)
                a[i] |= (uns(A[j]>=c))<<(j-L);
        }
        for(int r=0;r<w;++r) if(!vec[r].empty()) {
            int cnt=m;
            for(int i=1;i<=cnt;++i) {
                rec[i].clear();
                int R=min(i*w+r,n), L=(i-1)*w+1+r; b[i]=0;
                for(int j=L; j<=R; ++j)
                    b[i] |= (uns(B[j]>=c))<<(j-L);
            }
            for(const auto& t:vec[r]) {
                int L=bl[t.p1], R=bl[t.p1+t.L-1];
                if(t.p1%w!=1) ++L;
                if((t.p1+t.L-1)%w!=0) --R;
                if(L>R) continue;
                int ql = (t.p2-1-r)/w+1;
                if(t.p2<=r) ql=1;
                else if((t.p2-r)%w!=1) ++ql;
                int qr = (t.p2+t.L-2-r)/w+1;
                if((t.p2+t.L-1-r)%w!=0) --qr;
                rec[(ql-L+cnt)%cnt+1].emplace_back((Node){R,1,t.id});
                if(L>1) rec[(ql-L+cnt)%cnt+1].emplace_back((Node){L-1,-1,t.id});
            }
            for(int i=1;i<=cnt;++i) {
                sort(rec[i].begin(),rec[i].end(),
                [](const Node& x,const Node& y) { return x.pos<y.pos; });
                int cur=-1, siz=rec[i].size(), pre=0, k=i; if(!siz) continue;
                for(int j=1;j<=cnt;++j) {
                    pre += __builtin_popcountll(a[j]^b[k]);
                    while(cur+1<siz && rec[i][cur+1].pos==j)
                        ++cur, ans[rec[i][cur].id] += rec[i][cur].coe*pre;
                    ++ k; if(k>cnt) k=1;
                }
            }
        }
    }
    for(int r=0;r<w;++r) for(const auto& t:vec[r]) {
        if(bl[t.p1]==bl[t.p1+t.L-1]) {
            if(t.L==w) continue;
            for(int i=t.p1;i<=t.p1+t.L-1;++i)
                ans[t.id] += Abs(A[i]-B[i-t.p1+t.p2]);
            continue;
        }
        if(t.p1%w!=1) {
            int R = min(n,((t.p1-1)/w+1)*w);
            for(int i=t.p1;i<=R;++i)
                ans[t.id] += Abs(A[i]-B[i-t.p1+t.p2]);
        }
        if((t.p1+t.L-1)%w!=0) {
            int L = (bl[t.p1+t.L-1]-1)*w+1;
            for(int i=L;i<=t.p1+t.L-1;++i)
                ans[t.id] += Abs(A[i]-B[t.p2-t.p1+i]);
        }
    }
    for(int i=1;i<=q;++i) print(ans[i],'\n');
    return 0;
}