[学习笔记] 圆方树

\(\text{0x00.}\) 前言

突然发现整个机房似乎只有我不会圆方树了，而且最近模拟赛圆方树出现的次数令人咋舌，所以跑来学一下。才不是因为补不来题呢草。

\(\text{0x01.}\) 广义圆方树

定义

• 在圆方树中，原来的每个点对应一个 圆点，每一个点双对应一个 方点；
• 而对于每一个点双连通分量，它对应的方点向这个点双连通分量中的每个点连边；
• 圆方树中每条边连接一个圆点和一个方点。且若一个圆点连接多个方点，这个圆点在原图上的点为这些点双之间的割点。

需要注意的是，圆方树点数小于 \(2n\)，这受点双个数的限制。

\(\text{oi-wiki}\) 上的图应该不会挂吧（

构造

inline void addEdge(int u,int v) {
	e[u].emplace_back(v), e[v].emplace_back(u);
}
void tarjan(int u,int fa) {
	dfn[stk[++tp]=u] = low[u] = ++idx;
	for(const auto& v:E[u]) if(v^fa) {
		if(!dfn[v]) {
			tarjan(v,u), low[u]=min(low[u],low[v]);
			if(low[v]>=dfn[u]) {
				addEdge(++cnt,u); 
				while(stk[tp]^v) addEdge(cnt,stk[tp--]);
				addEdge(cnt,stk[tp--]);
			}
		} else low[u] = min(low[u],dfn[v]);
	}
} // it is senseless to keep the orphan

快来做题！

例 1. \(\text{[APIO 2018] Duathlon}\)

题意简述：给出无向图，求 \((s,c,f)\) 三元组的个数，代表从 \(s\) 出发经过 \(c\) 到达 \(f\)（不能重复经过点）。

考虑固定 \(s,f\)，有多少个 \(c\) 满足条件 —— 事实上，就是在建出圆方树后，\(s,f\) 所属的点双之间的点双中的点。这其实从感性上来看是非常合理的，考虑一个点双 \(b\) 和一个在它外面的点 \(a\)，那么从 \(b\) 中 任意 点出发走到 \(a\) 都无法 不经过曾经走过的点 回来了。

可是我们该如何计算贡献呢？将方点赋值为它代表的点双的大小，圆点赋值为 \(-1\)。\(-1\) 如何理解？还是看一张图：

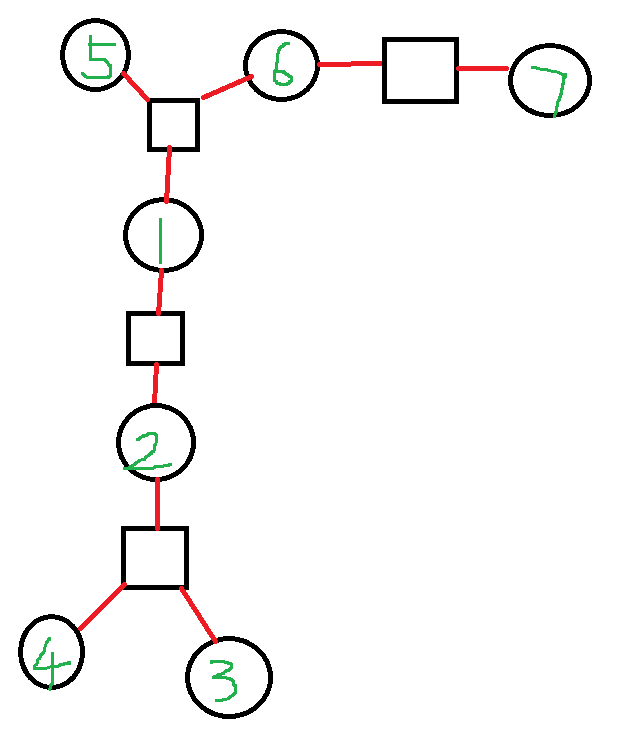
假设 \(s=4,f=5\)，可以发现 \(1,2\) 被相邻方点计算了两次，所以需要减去。由于路径两端一定是圆点，且圆点方点交错，所以这个玩意是对的。

现在问题实际上转化成了每个点会被路径计算多少次，树形 \(\mathtt{dp}\) 即可。

---

例 2. \(\text{CF487E Tourists}\)

题意简述：给定一张简单无向连通图，要求支持两种操作：

1. 修改一个点的点权；
2. 询问两点之间所有简单路径上点权的最小值。

运用上文的结论，可以直接将在方点维护一个 \(\text{multiset}\) 用来维护对应点双，然后用树剖维护。

问题在于，当修改被包含在多个点双中的割点时（比如菊花图），复杂度就会直接升天。这里有一个经典的 \(\rm trick\)：方点不维护父亲的权值，这样圆点就只会修改自己的父亲。显然只有当 \(\rm lca\) 为方点时查询会出错，补上方点父亲的点权即可。

---

例 3. \(\text{[SDOI 2018] }\)战略游戏

题意简述：给出一个简单无向连通图。有 \(q\) 次询问，每次给出一个点集 \(S\)，问有多少个点 \(u\) 满足 \(u\notin S\) 且删掉 \(u\) 之后 \(S\) 中的点不全在一个连通分量中。

容易发现，"\(S\) 中的点不全在一个连通分量中" 相当于存在 \(u,v\in S\)，使得 \(u,v\) 之间所有的简单路径都断开。所以相对 \(u,v\) 而言，它们各自所在点双之间的圆点即为合法切割点，那么就建出圆方树。

那么实际上是计算 \(S\) 中点在树上形成的最小连通块中的圆点个数。先给出计算方法：预处理根到每个点圆点个数 \(\rm val\)，将 \(S\) 中点按 \(\rm dfs\) 序排序，答案就是

\[-|S|+[\text{lca}(s_1,s_{|S|})\le n]+\frac{1}{2}\cdot \sum_{i=1}^{|S|}\text{val}_{s_i}+\text{val}_{s_{i+1}}-2\cdot \text{val}_{\text{lca}(s_i,s_{i+1})} \]

其中 \(s_{|S|+1}=s_1\).

给出一个理解的方法：计算 \(\rm val\) 时是将权值挂在 \(u\) 与父亲的边上，且我们实际上是在模拟 \(\rm dfs\) 的过程。每次相邻点的匹配，实际上都是从某个子树走出来，再走进某个子树，最后从最后一个点走回第一个点，接起来就是从 \(\text{lca}(s_1,s_{|S|})\) 为根，进行一个 \(\rm dfs\)！可以发现，每个点会被计算两次。同时也能发现，我们并没有计算 \(\text{lca}(s_1,s_{|S|})\) 的贡献，所以要进行特判。

---

例 4. \(\text{Chef and Sad Pairs}\)

不妨分颜色来考虑这个问题：那么建出圆方树，由于点 \(x\) 而悲伤的对数就相当于在 \(x\) 的不同子树中选点对（不妨将父亲也设想成 \(x\) 的子树）。但是这个 \(\rm dfs\) 复杂度是均摊的，所以需要建虚树求解。

不过还有一个问题：对于 "祖先 - 子孙" 关系中的 \(u,v\)（假设 \(u,v\) 同色，且它们之间没有其它颜色的点），它们之间的点没有统计这个颜色的答案！所以还需要做一个链上的差分。好水啊。

还是放一份代码吧：\(\text{Submission.}\)

另外还可以启发式合并：\(\text{Solution.}\)

---

\(\text{0x02.}\) 狭义圆方树

定义

不是很明白自己为什么还要划分出一个分类。

• 现在保证无向图为仙人掌森林。仙人掌：每条边最多属于一个环的无向连通图；
• 可以发现，此时每个点双都对应一个简单环，这样就可以将仙人掌问题转化成基环树上的问题求解，就像这样：

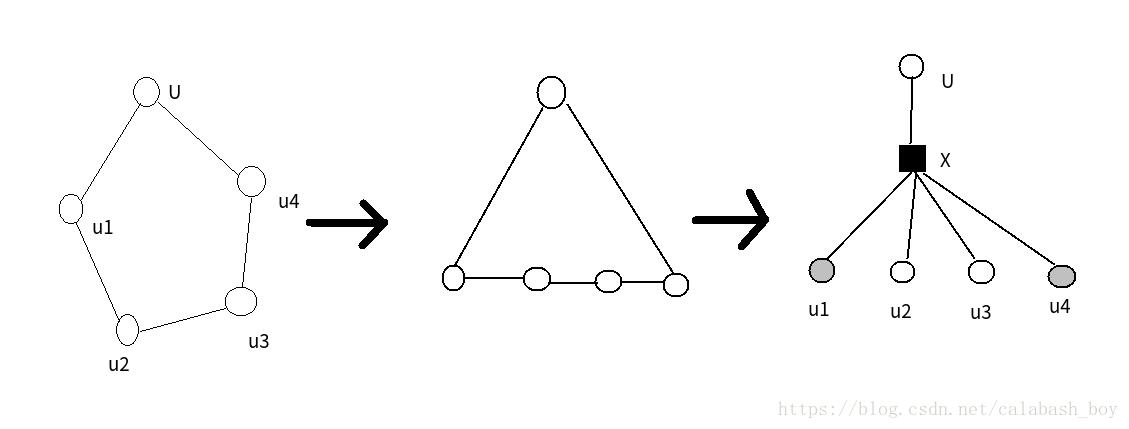
构造

void tarjan(int u,int fa) {
	dfn[u]=low[u]=++idx, stk[++tp]=u;
	for(const auto& v:G[u]) if(v^fa) {
		if(!dfn[v]) {
			tarjan(v,u), low[u]=min(low[u],low[v]);
			if(low[v]==dfn[u]) /* 圆方边 */;
            else if(low[v]>dfn[u]) /* 圆圆边 */;
		} else low[u] = min(low[u],dfn[v]);
	} 
}

快来做题！

例 1. \(\text{[BZOJ 4316] }\)小$\ \rm C\ $的独立集

首先，如果这是树形结构，可以设 \(dp(i,0/1)\) 求解。现在问题迁移到了仙人掌上，先建出圆方树，对于圆点与圆点的父子关系还是照样 \(\mathtt{dp}\)，否则我们处理方点的 \(\mathtt{dp}\) 值：由于原先点双是一个环，所以 \(0/1\) 状态实际上是边界两点均不选/选了至少一个边界。

---

例 2. \(\text{[SHOI 2008] }\)仙人掌图\(\text{ II}\)

这道题写了个惊天大巨坑：如果不重构树，那么圆圆边很容易被忽略！一定要记得 在圆圆边处将 \(\rm tp\) 减一！

---

例 3. \(\text{[HAOI 2016] }\)地图

首先进行题意的转化，发现要求的实际上是点 \(x\) 在圆方树的子树中，油腻度 \(\le y\) 品尝次数为奇/偶数的拉面品种。

对于子树问题，一个角度是 \(\text{dsu on tree / }\)线段树合并，也就是对子树直接搞；另一个角度就是用 \(\rm dfs\) 序将其转化为序列上的问题，就可以用扫描线（这题是不行的）\(\text{/ }\)分块之类的算法。

这里仔细讲一下分块做法。品尝次数为奇/偶数是很好统计的，关键是怎么搞 "油腻度 \(\le y\)" 的限制。可以想到用树状数组，但这样修改复杂度就变成了 \(\mathcal O(n\sqrt n\log n)\) 的玩意。事实上可以使用值域分块（窝分块真的太弱了，还是第一次见 qwq），定义 \(s(b,0/1)\) 为权值属于第 \(b\) 个块的出现次数为偶/奇数的品种数，单次修改即可做到 \(\mathcal O(1)\)，单次查询是 \(\mathcal O(\sqrt n)\) 的。

代码还都没写呢，等有空了再写吧咕咕咕。