建树
对于维护长度为 (n) 的序列,底层至少 (n+2) 个点。(t_{N+i}) 就代表下标 (i) 对应的叶子节点。底层的第一个节点的编号就是 (N),它是一个虚点。
计算一下可知 (N) 最多增加到 (2n+2),由于我们需要用到 (t_{N+n+1})(为什么后面再说),所以大约开三倍空间即可。
for(N=1;N<n+2;N<<=1);
for(int i=1;i<=n;++i)
t[N+i]=read(9);
for(int i=N-1;i;--i) // 注意从 N-1 开始更新,否则会越界
t[i]=t[i<<1]+t[i<<1|1];
单点修改,区间查询
void change(int o,int k) {
for(t[N+o]=k,o=N+o>>1;o;o>>=1)
t[o]=t[o<<1]+t[o<<1|1];
}
建立两个哨兵节点 (l,r) 代表区间 ([L,R]) 的 (L-1,R+1) 两个点。两个哨兵同时上移,如果 (l) 是左儿子,就将它对应的右儿子加入贡献。(r) 同理。
由于 ([L,R]) 可能取到 ([1,n]),所以 (t_N,t_{N+n+1}) 这两个虚点是必要的。
int ask(int l,int r) {
int ret=0;
for(l=N+l-1,r=N+r+1;l^r^1;l>>=1,r>>=1) {
if(~l&1) ret+=t[l^1];
if(r&1) ret+=t[r^1];
}
return ret;
}
区间修改,区间查询
先放一张图吧:
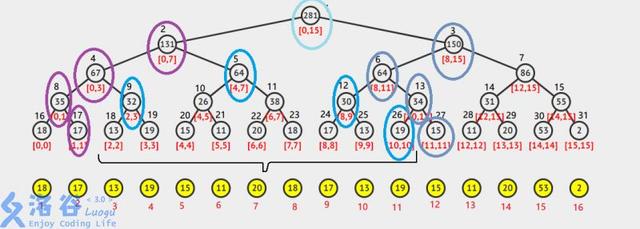
懒标记
维护 (t) 数组为区间和,(la) 数组是可持久化懒标记。
统计 (ls,rs) 分别为 (l,r) 向上跳时经过的 区间内 的点的个数,( ext{all}) 维护 (l,r) 跳跃当前层的节点个数。 当 (l,r) 成为某点的左右儿子时,也要继续往上更新。
void modify(int l,int r,int k) {
int ls=0,rs=0,all=1;
for(l=N+l-1,r=N+r+1;l^r^1;l>>=1,r>>=1,all<<=1) {
t[l]+=k*ls,t[r]+=k*rs; // 此时的 ls,rs 已经是 l,r 的儿子部分了
if(~l&1) {
la[l^1]+=k; t[l^1]+=k*all;
ls+=all;
}
if(r&1) {
la[r^1]+=k; t[r^1]+=k*all;
rs+=all;
}
}
for(;l;l>>=1,r>>=1)
t[l]+=k*ls,t[r]+=k*rs;
}
询问同理。对于不查询完整区间的,用懒标记贡献;反之直接加上 (t) 数组即可。
int ask(int l,int r) {
int ls=0,rs=0,all=1,ret=0;
for(l=N+l-1,r=N+r+1;l^r^1;l>>=1,r>>=1,all<<=1) {
ret+=la[l]*ls+la[r]*rs;
if(~l&1) ret+=t[l^1],ls+=all;
if(r&1) ret+=t[r^1],rs+=all;
}
for(;l;l>>=1,r>>=1)
ret+=la[l]*ls+la[r]*rs;
return ret;
}
差分
看了半天没有懂,于是就 咕咕咕 了。
区间修改,单点查询
此时将原数组当作懒标记数组来使用即可。代码十分简单。需要注意的是修改时,在 (l,r) 成为某点的左右儿子后就不再修改了。画画图可以知道此时已经将所修改区间到根的路径都打上了懒标记。
void modify(int l,int r,int k) {
for(l=N+l-1,r=N+r+1;l^r^1;l>>=1,r>>=1) {
if(~l&1) t[l^1]+=k;
if(r&1) t[r^1]+=k;
}
}
查询时将叶子到根的路径上懒标记累加即可。
int ask(int x) {
int ret=0;
for(x=N+x;x;x>>=1) ret+=t[x];
return ret;
}