题目链接
翻译
给你一棵树, 让你在这棵树上选择恰好k个点, 这k个点是发展工业的, 然后其余的n - k个点发展旅游业。
但是根节点(约定1号节点是根节点)例外, 它可以发展旅游业也可以发展工业(不过后面会发现这条件没啥用。。)。
假设x是你选出来的k个点中的一个, 对于所有的x, 你需要求出每个节点x到根节点1会经过的 发展旅游业 的节点个数(cnt_i), 然后对cnt求和,
求和的结果设为sum, 你需要找到这样的k个节点的安排, 使得sum的值最大。
题解
所以, 为啥根节点可以发展旅游业或者工业这个信息没用呢? 因为你会发现不管什么情况下, 让根节点发展旅游业总是更好的。
这样工业节点能多算一次旅游节点嘛。
然后就是自己画画图模拟一下了, 会发现, 你肯定是想选出来的工业结点越靠近最底层越好(实际上是, 离根节点越远越好)。
以下图为例
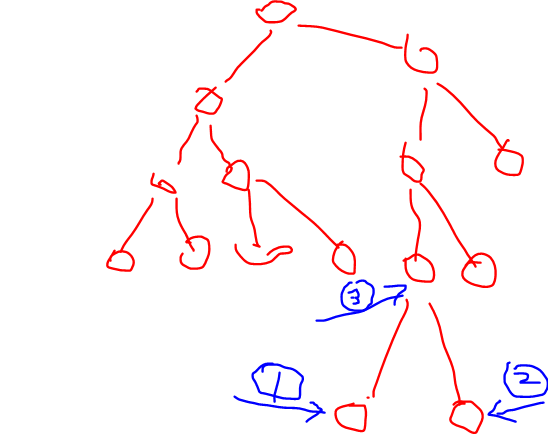
你肯会先选离根节点最远的, 也就是用蓝笔标记的①号节点, 然后是②号, 这两个点会经过的旅游节点的个数就是它们的树的高度。
但是有个问题, 最先选出来的两个节点很好办, 它们也没有分支什么的, 经过的旅游节点个数很好算,
但是如果选③号节点的话, 怎么办呢? 选择它的话, 会让它底下所有的节点对答案的贡献都减少1, 这点没错。
那, 会不会下面有哪个节点没有选呢? 肯定不会的! 我们可以由节点从高到低排序, 这样就能保证下面的节点先被选到。
因为底下所有的节点对答案贡献都会减少1, 所以选择了这个节点x对答案的贡献就是height[x] - _size[x] - 1, 这里的
height[x]表示树的高度, _size[x]表示以x为根的子树的大小(包括x)。
所以, 处理出来这个数组, 逆序排序, 然后选最大的k个累加起来就行。
题解中学来的一个性质 :一个旅游节点上面, 不可能存在有一个工业节点, 因为那样的话, 旅游节点和工业节点直接能调换一下, 这样工业节点就能多
累加一个旅游节点的值, 更优了。
所以类似B题, 旅游节点都是在树的路径上连续的一些节点。
代码
#include<bits/stdc++.h>
#define ll long long
#define rei(x) scanf("%d",&x)
#define rel(x) scanf("%I64d",&x)
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
using namespace std;
const int N = 2e5;
int n,k;
vector<int> g[N+10];
int _size[N+10],_height[N+10];
int p[N+10];
void dfs(int x,int fa){
_size[x] = 1;
int len = g[x].size();
rep1(i,0,len-1){
int y = g[x][i];
if (y==fa) continue;
_height[y] = _height[x] + 1;
dfs(y,x);
_size[x] += _size[y];
}
p[x] = _height[x]-(_size[x]-1);
}
int main(){
#ifdef LOCAL_DEFINE
freopen("D:\rush.txt","r",stdin);
#endif
ios::sync_with_stdio(0),cin.tie(0);
cin >> n >> k;
rep1(i,1,n-1){
int x,y;
cin >> x >> y;
g[x].push_back(y);
g[y].push_back(x);
}
_height[1] = 0;
dfs(1,0);
sort(p+1,p+1+n);
reverse(p+1,p+1+n);
ll sum = 0;
rep1(i,1,k){
sum = sum + p[i];
}
cout<<sum<<endl;
return 0;
}