【题目翻译】
给你个蛇形的图...你每次可以到右边或者下边一个相邻的格子。 问你从起点到终点的路径上遇到的和有多少种可能。【题解】
首先明确一件事情啊,绝对不是直接输出从起点到终点的不同走法个数哦。比如这张图的情况:
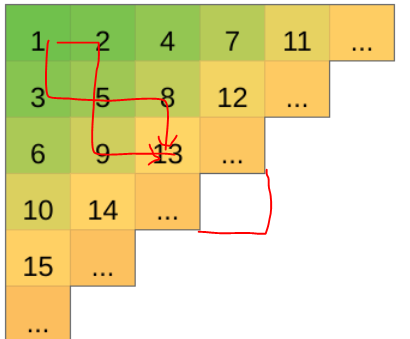
显然这两种是不同的走法但是和是一样的。
我们会发现,如果我们从起点一直往右走,然后一直往下走,得到的和肯定是最小的,记为min。
如果从起点一直往下走,然后一直往右走,得到的和肯定是最大的,记为max。
然后,通过观察,会发现,我们是有办法让走过的路径从min一直变化到max的,而且每次只需要递增1.如下图,
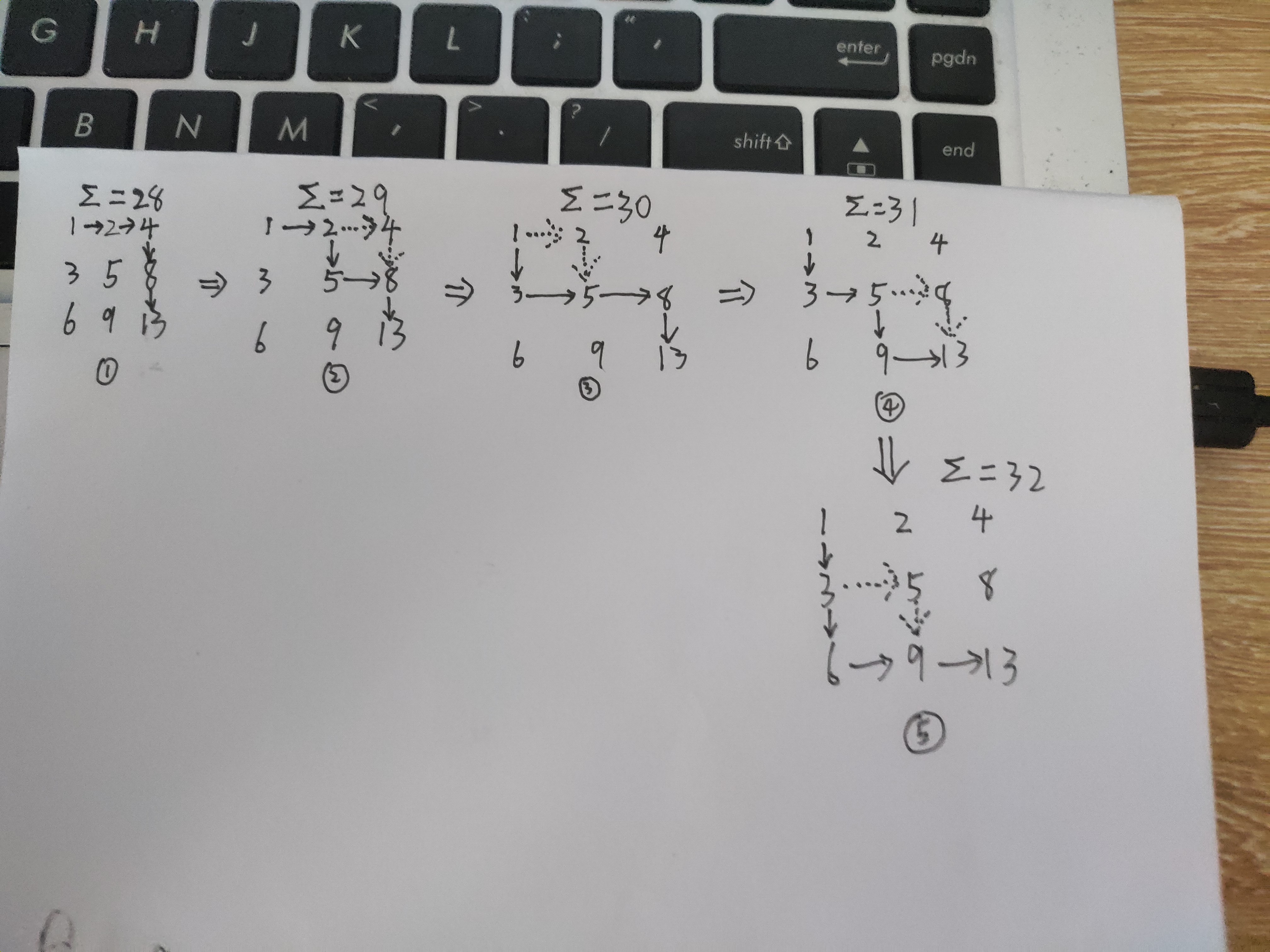
主要就是利用了,对角往左下角拐个弯,值只会递增1这个性质。
然后每行从最右边到最左边"拐弯",一共就能拐△x△y次,然后加上最小值的那一条路径,总共就是△x△y+1啦。
【代码】
#include<bits/stdc++.h>
#define ll long long
#define rei(x) scanf("%d",&x)
#define rel(x) scanf("%I64d",&x)
#define rep1(i,a,b) for (int i = a;i <= b;i++)
#define rep2(i,a,b) for (int i = a;i >= b;i--)
using namespace std;
const int N = 1e5;
ll x1,y1,x2,y2;
int main(){
#ifdef LOCAL_DEFINE
freopen("D:\rush.txt","r",stdin);
#endif
int T;
rei(T);
while (T--){
rel(x1);rel(y1);rel(x2);rel(y2);
ll tmp = (x2-x1)*(y2-y1)+1;
printf("%lld
",tmp);
}
return 0;
}