CodeForces 778D Parquet Re-laying 构造

题意：

有两个(n imes m)的矩阵(A,B)，都是由(1 imes 2)的砖块铺成，代表初始状态和结束状态
有一种操作可以把两个砖块拼成的(2 imes 2)的矩形旋转(90^{circ})

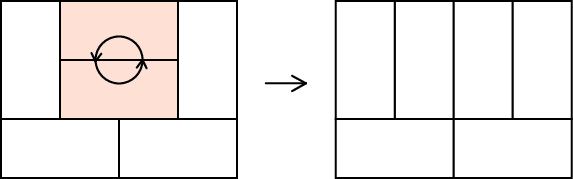
问如何操作才能使初始状态转化为结束状态，无解输出(-1)

分析：

不妨假设(m)为偶数，否则可以旋转整个矩阵使得矩阵的列数为偶数
先找一个中间过度状态矩阵(C)，它的每个砖块都是水平方向的
求出(A o C)和(B o C)的操作序列，因为操作是可逆的，所以就得到了(A o C o B)的操作序列

从第一行开始逐个扫描，遇到一个竖直方向的砖块就将它旋转，这是可能有两种情况：

• 右边的砖块也是竖直方向的，那么可以直接旋转
• 右边砖块是水平的，那么就递归到子问题：将右边的水平砖块先旋转过来，再一起旋转

算法的正确性不会证=_=

#include <cstdio>
#include <algorithm>
#include <vector>
#include <map>
using namespace std;

const int maxn = 60;
typedef pair<int, int> PII;
#define ALL(x) (x).begin(), (x).end()

int n, m, Max;
char s1[maxn][maxn], s2[maxn][maxn];
vector<PII> a, b;

void rotate(char s[][maxn], int x, int y) {
	if(s[x][y] == 'U') {
		s[x][y] = s[x+1][y] = 'L';
		s[x][y+1] = s[x+1][y+1] = 'R';
	} else {
		s[x][y] = s[x][y+1] = 'U';
		s[x+1][y] = s[x+1][y+1] = 'D';
	}
}

bool check(char s[][maxn], int x, int y) {
	if(s[x][y] == s[x][y+1] && s[x][y] == 'U' && s[x+1][y] == s[x+1][y+1] && s[x+1][y] == 'D') return true;
	if(s[x][y] == s[x+1][y] && s[x][y] == 'L' && s[x][y+1] == s[x+1][y+1] && s[x][y+1] == 'R') return true;
	return false;
}

bool adjust(char s[][maxn], int x, int y, int flag, vector<PII>& a) {
	if(x + 1 >= n || y + 1 >= m) return false;
	if(check(s, x, y)) {
		rotate(s, x, y);
		a.emplace_back(x, y);
		return true;
	} else {
		if(!adjust(s, x+1-flag, y+flag, flag^1, a)) return false;
		rotate(s, x, y);
		a.emplace_back(x, y);
		return true;
	}
}

void op(char& c) {
	switch(c) {
		case 'L': c = 'U'; break;
		case 'U': c = 'L'; break;
		case 'R': c = 'D'; break;
		case 'D': c = 'R'; break;
	}
}

void change(char s[][maxn]) {
	for(int i = 0; i < n; i++)
		for(int j = 0; j < m; j++) op(s[i][j]);
	for(int i = 0; i < Max; i++)
		for(int j = 0; j < i; j++)
			swap(s[i][j], s[j][i]);
}

int main()
{
	scanf("%d%d", &n, &m);
	for(int i = 0; i < n; i++) scanf("%s", s1[i]);
	for(int i = 0; i < n; i++) scanf("%s", s2[i]);
	Max = n > m ? n : m;
	bool changed = false;
	if(m & 1) { change(s1); change(s2); swap(n, m); changed = true; }

	for(int i = 0; i < n; i++) {
		for(int j = 0; j < m; j += 2) {
			if(s1[i][j] != 'L') {
				if(!adjust(s1, i, j, 1, a)) { puts("-1"); return 0; }
			}
			if(s2[i][j] != 'L') {
				if(!adjust(s2, i, j, 1, b)) { puts("-1"); return 0; }
			}
		}
	}

	reverse(ALL(b));
	a.insert(a.end(), ALL(b));
	printf("%d
", (int)a.size());
	for(pair<int, int> t : a) {
		if(changed) swap(t.first, t.second);
		printf("%d %d
", t.first + 1, t.second + 1);
	}

	return 0;
}