SPOJ FFT TSUM

第一道FFT的题目。

在网上找了很多FFT的资料，但一直都看不懂，最后是看算法导论学的FFT，算法导论上面写的很详细，每一步推导过程都有严格的证明。

下面说这道题

题意：

给一个序列s，有n个不互相同的整数。现在从这个序列中选出一个包含3个不同的整数的集合，对于他们的和为sum来说，求一共有多少种选法。(注意：3个数的先后顺序都看做一种选法)

分析：

构造一个多项式A(x)，这n个数作为多项式的指数。

A³(x)中的每一项的指数对应三个数的和，前面的系数是取数的方案数。

然而这并不是题目所求，这样的选法是任意取三个数，可能相同可能不同。

其中多计算了不合法的方案：

任意取三个数的方案数 = 取三个相同的数 + 取两个相同的数和另一个不同的数 + 三个互不相同的数

用式子表达出来就是： (图片来自叉姐PPT)

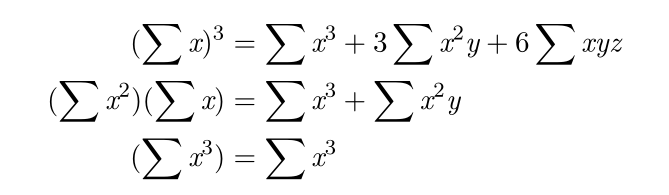
整理一下，答案就是：

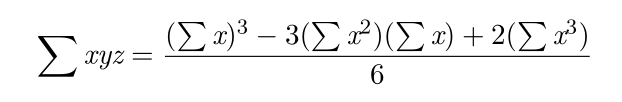
#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <complex>
#include <cmath>
using namespace std;

typedef long long LL;
const double PI = acos(-1.0);
typedef complex<double> Complex;

const int maxn = (1 << 17);

void FFT(Complex P[], int n, int oper)
{
    for(int i = 1, j = 0; i < n - 1; i++)
    {
        for(int s = n; j ^= s >>= 1, ~j & s; );
        if(i < j) swap(P[i], P[j]);
    }

    int log = 0;
    while((n & (1 << log)) == 0) log++;
    for(int s = 0; s < log; s++)
    {
        int m = (1 << s);
        int m2 = m * 2;
        Complex wm = Complex(cos(PI / m), sin(PI / m) * oper);
        for(int k = 0; k < n; k += m2)
        {
            Complex w(1, 0);
            for(int j = 0; j < m; j++, w = w * wm)
            {
                Complex t = w * P[k + j + m];
                Complex u = P[k + j];
                P[k + j] = u + t;
                P[k + j + m] = u - t;
            }
        }
    }

    if(oper == -1) for(int i = 0; i < n; i++) P[i].real() /= n;
}

int A[maxn], A2[maxn], A3[maxn];
Complex a[maxn], b[maxn];

int main()
{
    int n; scanf("%d", &n);
    while(n--)
    {
        int x; scanf("%d", &x);
        x += 20000;
        A[x]++;
        A2[x*2]++;
        A3[x*3]++;
    }
    for(int i = 0; i < maxn; i++) a[i] = A[i], b[i] = A2[i];

    FFT(a, maxn, 1);
    FFT(b, maxn, 1);
    for(int i = 0; i < maxn; i++) a[i] = a[i] * (a[i] * a[i] - b[i] * 3.0);
    FFT(a, maxn, -1);

    for(int i = 0; i < maxn; i++)
    {
        LL ans = (LL)((a[i].real() + 0.5) + A3[i] * 2) / 6;
        if(ans > 0) printf("%d : %lld
", i - 60000, ans);
    }

    return 0;
}