题意:
根据离散数学的内容知道,一个二元关系是一个二元有序组<x, y>的集合。
然后有一些特殊的二元关系,比如等价关系,满足三个条件:
- 自反性,任意的x,都有二元关系<x, x>
- 对称性,如果有<x, y>则有<y, x>
- 传递性,如果有<x, y>和<y, z>,则有<x, z>
现在要统计满足后两条,但不满足第一个条件的二元关系的个数。
题中的证明是对的:
If  , then
, then 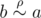 (according to property (2)), which means
(according to property (2)), which means  (according to property (3)).
(according to property (3)).
但是前提条件不一定存在,比如对于a,没有一个b满足 那么后面的推导就无从谈起了。
那么后面的推导就无从谈起了。
不妨把这些不和其他元素(包括自己)产生二元关系的元素称作「空」的。
只要至少有一个「空」的元素,而且其他的元素都在某个等价类里面,就满足题目中的要求。
枚举非「空」元素的个数k(1 ≤ k ≤ n),选出k个元素有C(n, k)中方案,再乘上将k个元素划分为若干个等价类的方案数eq[k],累加起来就是答案。
eq数组可以这样计算:
设d(i, j)为将i个元素划分为j个不同等价类的方案数,d(i, j) = d(i-1, j) * j + d(i-1, j-1) //考虑第i个数加入已有的j个等价类,或者自己成为一个新的等价类
那么eq[i] = sum{ d(i, j) | 0 ≤ j ≤ i }

1 #include <iostream> 2 #include <cstdio> 3 #include <cstring> 4 #include <algorithm> 5 using namespace std; 6 7 typedef long long LL; 8 9 const int maxn = 4000 + 10; 10 const LL MOD = 1000000007; 11 12 LL C[maxn][maxn], d[maxn][maxn]; 13 14 void add(LL& x, LL y) 15 { 16 x += y; 17 if(x >= MOD) x -= MOD; 18 } 19 20 int main() 21 { 22 int n; scanf("%d", &n); 23 24 for(int i = 0; i <= n; i++) C[i][0] = C[i][i] = 1; 25 for(int i = 2; i <= n; i++) 26 for(int j = 1; j < i; j++) C[i][j] = (C[i-1][j] + C[i-1][j-1]) % MOD; 27 28 d[0][0] = 1; 29 for(int i = 1; i <= n; i++) 30 for(int j = 1; j <= i; j++) d[i][j] = (d[i-1][j] * j + d[i-1][j-1]) % MOD; 31 32 LL ans = 0; 33 for(int i = 0; i < n; i++) 34 { 35 LL eq = 0; 36 for(int j = 0; j <= i; j++) add(eq, d[i][j]); 37 ans = (ans + C[n][i] * eq) % MOD; 38 } 39 40 printf("%I64d ", ans); 41 42 return 0; 43 }
