AdaBoost算法原理
AdaBoost算法针对不同的训练集训练同一个基本分类器(弱分类器),然后把这些在不同训练集上得到的分类器集合起来,构成一个更强的最终的分类器(强分类器)。理论证明,只要每个弱分类器分类能力比随机猜测要好,当其个数趋向于无穷个数时,强分类器的错误率将趋向于零。AdaBoost算法中不同的训练集是通过调整每个样本对应的权重实现的。最开始的时候,每个样本对应的权重是相同的,在此样本分布下训练出一个基本分类器h1(x)。对于h1(x)错分的样本,则增加其对应样本的权重;而对于正确分类的样本,则降低其权重。这样可以使得错分的样本突出出来,并得到一个新的样本分布。同时,根据错分的情况赋予h1(x)一个权重,表示该基本分类器的重要程度,错分得越少权重越大。在新的样本分布下,再次对基本分类器进行训练,得到基本分类器h2(x)及其权重。依次类推,经过T次这样的循环,就得到了T个基本分类器,以及T个对应的权重。最后把这T个基本分类器按一定权重累加起来,就得到了最终所期望的强分类器。
AdaBoost算法的具体描述如下:
假定X表示样本空间,Y表示样本类别标识集合,假设是二值分类问题,这里限定Y={-1,+1}。令S={(Xi,yi)|i=1,2,…,m}为样本训练集,其中Xi∈X,yi∈Y。
① 始化m个样本的权值,假设样本分布Dt为均匀分布:Dt(i)=1/m,Dt(i)表示在第t轮迭代中赋给样本(xi,yi)的权值。
② 令T表示迭代的次数。
③ For t=1 to T do
根据样本分布Dt,通过对训练集S进行抽样(有回放)产生训练集St。
在训练集St上训练分类器ht。
用分类器ht对原训练集S中的所有样本分类。
得到本轮的分类器ht:X →Y,并且有误差εt=Pri-Di[ht(xi) ≠yi]。
令αt=(1/2)ln[(1-εt)/ εt]。
更新每个样本的权值,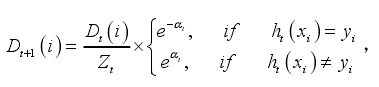
其中,Zt是一个正规因子,用来确保ΣiDt+1(i)=1。
end for
④ 最终的预测输出为: