学习了一下费用流的做法,顺便学习了一下zkw(听说原始对偶是折中做法,这种没什么特点的就不学了),顺便研究了一下费用流的速度:(对于这题而言)upd抱歉我这个SLF优化写反了。。。然而反过来也只是跑了2s+的点快了0.3s+,所以区别不大
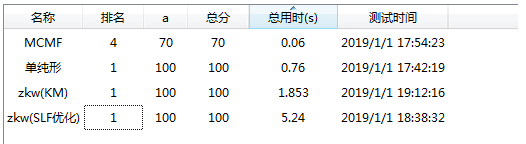
解决线性规划还是单纯形法优秀啊
zkw费用流适用费用值域较小,增广路径较短的图(二分图)
然后类似KM的写法是不资瓷边权为负的(懵逼)因为我尝试写了一会样例都过不了
然而实际上构出最长路径树直接跑最大费用最大流就好了。。。。
对于这道题费用流的做法:
还是先把原始问题转换成对偶问题(假如不转对偶应该也是同理的推),注意此时系数和约束常数项就互换了,也就是费用和至少安插的塔可以理解为互换了
此时把约束差分。差分有一个很优美的性质,每个柿子会被加一次减一次,如果我们把每个约束看成一个点,变量相当于流到这个约束又流走
那么把式子加起来每个变量和常数和等于0,联想到网络流的流量平衡
我们得到如下建图方法:
1:差分后的常数项若大于0,就从st连一条流量为该值费用无限的边,反之从该约束连向ed连一条流量为该值相反数费用无限的边,常数平衡
2:对于一个变量,差分后他是正值的约束连向差分后他是负值的约束,变量平衡
3:差分后相邻的两个约束由前一个连向后一个,流量无限费用为0:处理松弛变量的影响,和2同理
最后跑最大费用最大流

#include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; const double eps=1e-7; int n,m; double sum; double a[1100][11000],b[11000],c[1100]; void pivot(int o,int e) { c[o]/=a[o][e]; for(int i=1;i<=m;i++) if(i!=e)a[o][i]/=a[o][e]; a[o][e]=1/a[o][e]; for(int i=1;i<=n;i++) if(i!=o&&fabs(a[i][e])>eps) { c[i]-=c[o]*a[i][e]; for(int j=1;j<=m;j++) if(j!=e)a[i][j]-=a[o][j]*a[i][e]; a[i][e]*=-a[o][e]; } sum+=b[e]*c[o]; for(int i=1;i<=m;i++) if(i!=e)b[i]-=a[o][i]*b[e]; b[e]*=-a[o][e]; } void simplex() { int e,o; double d; while(1) { d=0; for(int i=1;i<=m;i++) if(b[i]>d)d=b[i],e=i; if(d==0)return ; d=(1<<30); for(int i=1;i<=n;i++) if(a[i][e]>eps&&d>c[i]/a[i][e]) d=c[i]/a[i][e],o=i; if(d==(1<<30)){sum=(1<<30);return ;} pivot(o,e); } } int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); int l,r; scanf("%d%d",&n,&m); for(int i=1;i<=n;i++)scanf("%lf",&c[i]); memset(a,0,sizeof(a)); for(int i=1;i<=m;i++) { scanf("%d%d%lf",&l,&r,&b[i]); for(int j=l;j<=r;j++)a[j][i]++; } simplex(); printf("%.0lf ",sum); return 0; }

#include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; const int inf=(1<<30)-1; struct node { int x,y,c,d,next; }a[310000];int len,last[21000]; void ins(int x,int y,int c,int d) { len++; a[len].x=x;a[len].y=y;a[len].c=c;a[len].d=d; a[len].next=last[x];last[x]=len; len++; a[len].x=y;a[len].y=x;a[len].c=0;a[len].d=-d; a[len].next=last[y];last[y]=len; } int st,ed; int pre[21000],c[21000],ans,d[21000]; int list[21000];bool v[21000]; bool spfa() { memset(d,63,sizeof(d));d[st]=0;c[st]=(1<<30); memset(v,false,sizeof(v));v[st]=true; int head=1,tail=2;list[1]=st; while(head!=tail) { int x=list[head]; for(int k=last[x];k;k=a[k].next) { int y=a[k].y; if(a[k].c>0&&d[y]>d[x]+a[k].d) { d[y]=d[x]+a[k].d; c[y]=min(a[k].c,c[x]); pre[y]=k; if(v[y]==false) { v[y]=true; list[tail]=y; tail++;if(tail==20100)tail=1; } } } v[x]=false; head++;if(head==20100)head=1; } if(d[ed]==d[0])return false; else { int y=ed;ans+=c[ed]*d[ed]; while(y!=st) { int k=pre[y]; a[k].c-=c[ed]; a[k^1].c+=c[ed]; y=a[k].x; } return true; } } int p[1100]; int main() { freopen("a.in","r",stdin); freopen("a.out","w",stdout); int n,m; scanf("%d%d",&n,&m); st=n+2,ed=n+3; len=1; for(int i=1;i<=n;i++) scanf("%d",&p[i]),ins(i,i+1,inf,0); for(int i=1;i<=n+1;i++) if(p[i]-p[i-1]>0)ins(st,i,p[i]-p[i-1],0); else ins(i,ed,p[i-1]-p[i],0); int l,r,d; for(int i=1;i<=m;i++) { scanf("%d%d%d",&l,&r,&d); ins(l,r+1,inf,-d); } while(spfa()); printf("%d ",-ans); return 0; }
 zkw(SLF)
zkw(SLF)
#include<cstdio> #include<iostream> #include<cstring> #include<cstdlib> #include<algorithm> #include<cmath> using namespace std; const int inf=(1<<30)-1; struct node { int x,y,c,d,next; }a[210000];int len,last[1100]; void ins(int x,int y,int c,int d) { len++; a[len].x=x;a[len].y=y;a[len].c=c;a[len].d=d; a[len].next=last[x];last[x]=len; len++; a[len].y=x;a[len].x=y;a[len].c=0;a[len].d=-d; a[len].next=last[y];last[y]=len; } int st,ed; int head,tail,list[1100]; bool v[1100]; int d[1100]; void spfa() { memset(v,false,sizeof(v));v[ed]=true; memset(d,-63,sizeof(d));d[ed]=0; head=1,tail=2;list[head]=ed; while(head!=tail) { int x=list[head]; for(int k=last[x];k;k=a[k].next) { int y=a[k].y; if(a[k^1].c>0&&d[y]<d[x]+a[k^1].d) { d[y]=d[x]+a[k^1].d; if(v[y]==false) { v[y]=true; list[tail]=y; tail++;if(tail==1050)tail=1; } } } v[x]=false; head++;if(head==1050)head=1; } } int ans; int findflow(int x,int f) { if(x==ed){ans+=d[st]*f;return f;} int s=0; for(int k=last[x];k;k=a[k].next) { int y=a[k].y; if(v[y]==false&&d[x]-a[k].d==d[y]&&a[k].c>0&&s<f) { v[y]=true; int t=findflow(y,min(a[k].c,f-s)); s+=t;a[k].c-=t;a[k^1].c+=t; } } return s; } bool adjust() { int tmp=-inf; for(int x=1;x<=ed;x++) if(v[x]==true) { for(int k=last[x];k;k=a[k].next) { int y=a[k].y; if(v[y]==false&&a[k].c>0) tmp=max(tmp,d[y]+a[k].d-d[x]); } } if(tmp==-inf)return false; for(int i=1;i<=ed;i++) if(v[i]==true)d[i]+=tmp; return true; } int c[1100]; int main() { int n,m; scanf("%d%d",&n,&m); st=n+2,ed=n+3; len=1; for(int i=1;i<=n;i++) scanf("%d",&c[i]),ins(i,i+1,inf,0); for(int i=1;i<=n+1;i++) if(c[i]-c[i-1]>0)ins(st,i,c[i]-c[i-1],0); else ins(i,ed,c[i-1]-c[i],0); int l,r,d; for(int i=1;i<=m;i++) { scanf("%d%d%d",&l,&r,&d); ins(l,r+1,inf,d); } ans=0; spfa(); do { do { memset(v,false,sizeof(v));v[st]=true; }while(findflow(st,inf)); }while(adjust()); printf("%d ",ans); return 0; }
