Codeforces Beat Round#57(Div.2)

A. Table

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Simon has a rectangular table consisting of n rows and m columns. Simon numbered the rows of the table from top to bottom starting from one and the columns — from left to right starting from one. We'll represent the cell on the x-th row and the y-th column as a pair of numbers (x, y). The table corners are cells: (1, 1), (n, 1), (1, m), (n, m).

Simon thinks that some cells in this table are good. Besides, it's known that no good cell is the corner of the table.

Initially, all cells of the table are colorless. Simon wants to color all cells of his table. In one move, he can choose any good cell of table (x₁, y₁), an arbitrary corner of the table (x₂, y₂) and color all cells of the table (p, q), which meet both inequations: min(x₁, x₂) ≤ p ≤ max(x₁, x₂), min(y₁, y₂) ≤ q ≤ max(y₁, y₂).

Help Simon! Find the minimum number of operations needed to color all cells of the table. Note that you can color one cell multiple times.

Input

The first line contains exactly two integers n, m (3 ≤ n, m ≤ 50).

Next n lines contain the description of the table cells. Specifically, the i-th line contains m space-separated integers a_i1, a_i2, ..., a_im. If a_ij equals zero, then cell (i, j) isn't good. Otherwise a_ij equals one. It is guaranteed that at least one cell is good. It is guaranteed that no good cell is a corner.

Output

Print a single number — the minimum number of operations Simon needs to carry out his idea.

Sample test(s)

input

3 3
0 0 0
0 1 0
0 0 0

output

4

input

4 3
0 0 0
0 0 1
1 0 0
0 0 0

output

2

Note

In the first sample, the sequence of operations can be like this:

• For the first time you need to choose cell (2, 2) and corner (1, 1).
• For the second time you need to choose cell (2, 2) and corner (3, 3).
• For the third time you need to choose cell (2, 2) and corner (3, 1).
• For the fourth time you need to choose cell (2, 2) and corner (1, 3).

In the second sample the sequence of operations can be like this:

• For the first time you need to choose cell (3, 1) and corner (4, 3).
• For the second time you need to choose cell (2, 3) and corner (1, 1).

/*************
AC
Time:2013-11-2
************/
#include <iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>

using namespace std;
int num[52][52];
int main()
{
    int n,m;
    while(scanf("%d %d",&n,&m)!=EOF)
    {
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                scanf("%d",&num[i][j]);
            }
        }
        int judge=0;
        for(int i=1;i<=m;i++)
        {
            if(num[1][i]==1)
            judge=1;
        }
        for(int i=1;i<=m;i++)
        {
            if(num[n][i]==1)
            judge=1;
        }
        for(int i=1;i<=n;i++)
        {
            if(num[i][1]==1)
            judge=1;
        }
        for(int i=1;i<=n;i++)
        {
            if(num[i][m]==1)
            judge=1;
        }
        if(judge==1)printf("2
");
        else printf("4
");
    }

    return 0;
}

 

 

B. Permutation

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

A permutation p is an ordered group of numbers p₁,   p₂,   ...,   p_n, consisting of n distinct positive integers, each is no more than n. We'll define number n as the length of permutation p₁,   p₂,   ...,   p_n.

Simon has a positive integer n and a non-negative integer k, such that 2k ≤ n. Help him find permutation a of length 2n, such that it meets this equation: .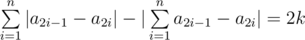

Input

The first line contains two integers n and k (1 ≤ n ≤ 50000, 0 ≤ 2k ≤ n).

Output

Print 2n integers a₁, a₂, ..., a_2n — the required permutation a. It is guaranteed that the solution exists. If there are multiple solutions, you can print any of them.

Sample test(s)

input

1 0

output

1 2

input

2 1

output

3 2 1 4

input

4 0

output

2 7 4 6 1 3 5 8

Note

Record |x| represents the absolute value of number x.

In the first sample |1 - 2| - |1 - 2| = 0.

In the second sample |3 - 2| + |1 - 4| - |3 - 2 + 1 - 4| = 1 + 3 - 2 = 2.

In the third sample |2 - 7| + |4 - 6| + |1 - 3| + |5 - 8| - |2 - 7 + 4 - 6 + 1 - 3 + 5 - 8| = 12 - 12 = 0.

/************
AC
Time:2013-11-2
*************/
#include <iostream>
#include<stdio.h>
#include<string.h>
int num[100100];

using namespace std;

int main()
{
    int n,k;
    while(scanf("%d%d",&n,&k)!=EOF)
    {
        for(int i=1;i<=2*n;i++)
        {
            num[i]=2*n-i+1;
        }
        for(int j=1;j<=k;j++)
        {
            int t=num[j*2];
            num[j*2]=num[j*2-1];
            num[j*2-1]=t;
        }
        for(int i=1;i<=2*n;i++)
        {
            if(i!=1)printf(" %d",num[i]);
            else printf("%d",num[i]);
        }
        printf("
");
    }
    return 0;
}

 

D. Pair of Numbers

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Simon has an array a₁, a₂, ..., a_n, consisting of n positive integers. Today Simon asked you to find a pair of integers l, r (1 ≤ l ≤ r ≤ n), such that the following conditions hold:

1. there is integer j (l ≤ j ≤ r), such that all integers a_l, a_l + 1, ..., a_r are divisible by a_j;
2. value r - l takes the maximum value among all pairs for which condition 1 is true;

Help Simon, find the required pair of numbers (l, r). If there are multiple required pairs find all of them.

Input

The first line contains integer n (1 ≤ n ≤ 3·10⁵).

The second line contains n space-separated integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁶).

Output

Print two integers in the first line — the number of required pairs and the maximum value of r - l. On the following line print all l values from optimal pairs in increasing order.

Sample test(s)

input

5
4 6 9 3 6

output

1 3
2 

input

5
1 3 5 7 9

output

1 4
1 

input

5
2 3 5 7 11

output

5 0
1 2 3 4 5 

Note

In the first sample the pair of numbers is right, as numbers 6, 9, 3 are divisible by 3.

In the second sample all numbers are divisible by number 1.

In the third sample all numbers are prime, so conditions 1 and 2 are true only for pairs of numbers (1, 1), (2, 2), (3, 3), (4, 4), (5, 5).

ps：开始脑残的写错了，没过。

/***************
AC
Time:2013-11-3
**********************/
#include <iostream>
#include<stdio.h>
#include<string.h>
#include<math.h>
int pre[300050];
int csn[300050];

using namespace std;

int main()
{
    int n;
    while(scanf("%d",&n)!=EOF)
    {
        int l,r;
        int tmp=0;
        int cnt=0;
        for(int i=1;i<=n;i++)
        scanf("%d",&pre[i]);
        for(int i=1;i<=n;i++)
        {
            l=r=i;
            while(l&&pre[l]%pre[i]==0)l--;
            while(r<=n&&pre[r]%pre[i]==0)r++;
            i=r;
            r=r-l-2;
            if(r>tmp)
            {
                tmp=r;
                cnt=0;
               // csn[cnt++]=l+1;
            }
            if(r==tmp)
            {
                csn[cnt++]=l+1;
                //printf("!!!
");
            }

        }
        printf("%d %d
",cnt,tmp);
        for(int i=0;i<cnt;i++)
        {
            if(i!=0)printf(" %d",csn[i]);
            else printf("%d",csn[i]);
        }
        printf("
");
    }
    return 0;
}