BZOJ3894 文理分科

文理分科是一件很纠结的事情！（虽然看到这个题目的人肯定都没有纠

结过）

小P所在的班级要进行文理分科。他的班级可以用一个n*m的矩阵进行

描述，每个格子代表一个同学的座位。每位同学必须从文科和理科中选择

一科。同学们在选择科目的时候会获得一个满意值。满意值按如下的方式

得到：

1．如果第i行第秒J的同学选择了文科，则他将获得art[i][j]的满意值，如

果选择理科，将得到science[i][j]的满意值。

2．如果第i行第J列的同学选择了文科，并且他相邻（两个格子相邻当且

仅当它们拥有一条相同的边）的同学全部选择了文科，则他会更开

心，所以会增加same_art[i][j]的满意值。

3．如果第i行第j列的同学选择了理科，并且他相邻的同学全部选择了理

科，则增加same_science[i]j[]的满意值。

小P想知道，大家应该如何选择，才能使所有人的满意值之和最大。请

告诉他这个最大值。

样例说明

1表示选择文科，0表示选择理科，方案如下：

1 0 0 1

0 1 0 0

1 0 0 0

N,M<=100,读入数据均<=500

感觉题目描述有点问题

不看题解根本不知道怎么建图。

分析：首先如果没有相邻全选情况，建图比较容易。文科与S相连，理科与T相连，求最小割，每条路径必定割掉一条边。

下面考虑相邻全选情况。相邻中有任意一人选文，就没有额外的理科加成。同理相邻任意一人选理，就没有额外的文科加成。根据这个可以这样建图，每个点再拆为P1，P2，如图：

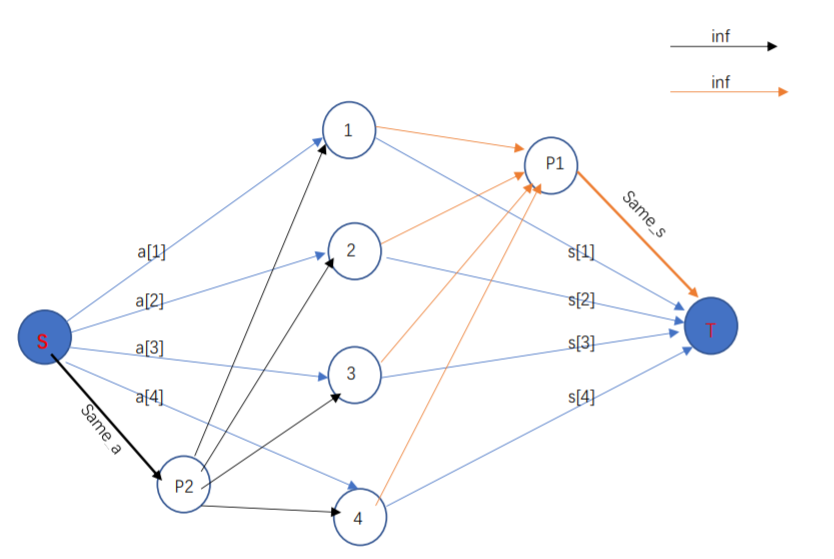
1，2，3，4为某个位置的相邻点。与P1相连，流量为inf，这样如果任意一个选文科（假设a[1]），即与S相连，必定会割掉Same_s这条边。因为选a[1],肯定没有s[1]，要保持不连通，最小割肯定割Same_s,不会割inf。同理对于Same_a,也一样。任意一个选理科（假设s[3]），与T相连，肯定没有a[3],要保持不连通，最小割肯定割Same_a，不会割inf。

这样建图满足了额外加成的控制。

直接用总的满意度-最小割即可

第一次知道拆点方法，P(i,j) = (i-1)*m+j，然后P1=P(i,j)+n*m P2=P(i,j)+2*n*m

  1 #include<bits/stdc++.h>
  2 using namespace std;
  3 #define P(i,j) (i-1)*m+j
  4 
  5 const int maxn=100010;
  6 const int maxm=400010;
  7 const int inf=0x3f3f3f3f;
  8 struct Edge{
  9     int to,next,cap,flow,cost;
 10 }edge[maxm];
 11 
 12 int tol;
 13 int head[maxn];
 14 int gap[maxn],dep[maxn],cur[maxn];
 15 int dir[][2]={0,0,1,0,-1,0,0,-1,0,1};
 16 void init() {
 17     tol=0;
 18     memset(head,-1,sizeof(head));
 19 }
 20 void addedge(int u,int v,int w,int rw=0) {
 21     edge[tol].to=v;edge[tol].cap=w;edge[tol].flow=0;
 22     edge[tol].next=head[u];head[u]=tol++;
 23     edge[tol].to=u;edge[tol].cap=rw;edge[tol].flow=0;
 24     edge[tol].next=head[v];head[v]=tol++;
 25 }
 26 
 27 int Q[maxn];
 28 void bfs(int start,int end) {
 29     memset(dep,-1,sizeof(dep));
 30     memset(gap,0,sizeof(gap));
 31     gap[0]=1;
 32     int front=0,rear=0;
 33     dep[end]=0;
 34     Q[rear++]=end;
 35     while(front!=rear) {
 36         int u=Q[front++];
 37         for(int i=head[u];i!=-1;i=edge[i].next) {
 38             int v=edge[i].to;
 39             if(dep[v]!=-1) continue;
 40             Q[rear++]=v;
 41             dep[v]=dep[u]+1;
 42             gap[dep[v]]++;
 43         }
 44     }
 45 }
 46 
 47 int S[maxn];
 48 int sap(int start,int end,int n) {
 49     bfs(start,end);
 50     memcpy(cur,head,sizeof(head));
 51     int top=0;
 52     int u=start;
 53     int ans=0;
 54     while(dep[start]<n) {
 55         if(u==end) {
 56             int minn=inf;
 57             int inser;
 58             for(int i=0;i<top;i++) {
 59                 if(minn>edge[S[i]].cap-edge[S[i]].flow) {
 60                     minn=edge[S[i]].cap-edge[S[i]].flow;
 61                     inser=i;
 62                 }
 63             }
 64             for(int i=0;i<top;i++) {
 65                 edge[S[i]].flow+=minn;
 66                 edge[S[i]^1].flow-=minn;
 67             }
 68             ans+=minn;
 69             top=inser;
 70             u=edge[S[top]^1].to;
 71             continue;
 72         }
 73         bool flag=false;
 74         int v;
 75         for(int i=cur[u];i!=-1;i=edge[i].next) {
 76             v=edge[i].to;
 77             if(edge[i].cap-edge[i].flow&&dep[v]+1==dep[u]) {
 78                 flag=true;
 79                 cur[u]=i;
 80                 break;
 81             }
 82         }
 83         if(flag) {
 84             S[top++]=cur[u];
 85             u=v;
 86             continue;
 87         }
 88         int minn=n;
 89         for(int i=head[u];i!=-1;i=edge[i].next) {
 90             if(edge[i].cap-edge[i].flow&&dep[edge[i].to]<minn) {
 91                 minn=dep[edge[i].to];
 92                 cur[u]=i;
 93             }
 94         }
 95         gap[dep[u]]--;
 96         if(!gap[dep[u]]) return ans;
 97         dep[u]=minn+1;
 98         gap[dep[u]]++;
 99         if(u!=start) u=edge[S[--top]^1].to;
100     }
101     return ans;
102 }
103 
104 int main() {
105     int n,m,x,sum;
106     while(~scanf("%d%d",&n,&m)) {
107         init();
108         sum=0;
109         int S=0,T=3*n*m+1;
110         for(int i=1;i<=n;i++) {
111             for(int j=1;j<=m;j++) {
112                 scanf("%d",&x);
113                 sum+=x;
114                 addedge(S,P(i,j),x);
115             }
116         }
117         for(int i=1;i<=n;i++) {
118             for(int j=1;j<=m;j++) {
119                 scanf("%d",&x);
120                 sum+=x;
121                 addedge(P(i,j),T,x);
122             }
123         }
124         for(int i=1;i<=n;i++) {
125             for(int j=1;j<=m;j++) {
126                 scanf("%d",&x);
127                 sum+=x;
128                 for(int k=0;k<5;k++) {
129                     int newx=i+dir[k][0];
130                     int newy=j+dir[k][1];
131                     if(newx<1||newx>n||newy<1||newy>m) continue;
132                     addedge(P(i,j)+2*n*m,P(newx,newy),inf);
133                 }
134                 addedge(S,P(i,j)+2*n*m,x);
135             }
136         }
137         for(int i=1;i<=n;i++) {
138             for(int j=1;j<=m;j++) {
139                 scanf("%d",&x);
140                 sum+=x;
141                 for(int k=0;k<5;k++) {
142                     int newx=i+dir[k][0];
143                     int newy=j+dir[k][1];
144                     if(newx<1||newx>n||newy<1||newy>m) continue;
145                     addedge(P(newx,newy),P(i,j)+n*m,inf);
146                 }
147                 addedge(P(i,j)+n*m,T,x);
148             }
149         }
150         printf("%d
",sum-sap(0,T,T+1));
151     }
152 }

BZOJ3894 文理分科

Description

Input

Output

Sample Input

Sample Output

HINT