终于又一次迎来了一道期望DP题，按照约定，小C把它贴了出来。
Description
你正在玩你最喜欢的电子游戏，并且刚刚进入一个奖励关。在这个奖励关里，系统将依次随机抛出k次宝物，每次你都可以选择吃或者不吃（必须在抛出下一个宝物之前做出选择，且现在决定不吃的宝物以后也不能再吃）。 宝物一共有n种，系统每次抛出这n种宝物的概率都相同且相互独立。也就是说，即使前k-1次系统都抛出宝物1（这种情况是有可能出现的，尽管概率非常小），第k次抛出各个宝物的概率依然均为1/n。 获取第i种宝物将得到Pi分，但并不是每种宝物都是可以随意获取的。第i种宝物有一个前提宝物集合Si。只有当Si中所有宝物都至少吃过一次，才能吃第i种宝物（如果系统抛出了一个目前不能吃的宝物，相当于白白的损失了一次机会）。注意，Pi可以是负数，但如果它是很多高分宝物的前提，损失短期利益而吃掉这个负分宝物将获得更大的长期利益。 假设你采取最优策略，平均情况你一共能在奖励关得到多少分值？
Input
第一行为两个正整数k和n，即宝物的数量和种类。以下n行分别描述一种宝物，其中第一个整数代表分值，随后的整数依次代表该宝物的各个前提宝物（各宝物编号为1到n），以0结尾。
Output
输出一个实数，保留六位小数，即在最优策略下平均情况的得分。
Sample Input
1 2
1 0
2 0
Sample Output
1.500000
HINT
1<=k<=100，1<=n<=15，分值为[-10^6,10^6]内的整数。
Solution
关于概率期望的题目让人头大，但是如果你还记得之前的口诀“概率正着做，期望倒着做”，这题就会变得很无脑。
很显然这题要我们求的是期望，所以我们倒着开始思考问题。
我们注意到n的范围小等于15，那还能是什么做法啊，当然是状压啊。
于是我们考虑设计状态，f[i][j]表示取了已经抛出i次物品，并且取了集合为j的物品至少1次，这之后按照最优策略能取到的期望值。
所谓最优策略，实际上就是比较转移代价和目标收益之间的大小关系，
假设我们在状态f[i][j]，假设可以取得物品x，我们就要斟酌一下取得x的代价和取得x之后的收益，
也就是比较-w[x]和f[i+1][j|ys[x]]的大小，
如果-w[x]<f[i+1][j|ys[x]]，也就是说收益更大，按照最优原则我们应该要取；（为什么是“应该”呢）
反之就是代价更大，按照最优原则我们肯定不能取，但是请注意，不取x也有一个收益，那就是f[i+1][j]。
不过就算取x的收益比代价大，但这两者的差值不一定大于不取x的收益，所以按照最优策略还是要对两者取一个max。
结合上面的思路来看，我们发现f[i][j]永远不可能是负数。
前面说的是能够取得物品x的情况，那么什么时候取不了物品x（未满足x的前提宝物集合）呢？
这种问题还用问？看看你自己设计的状态就知道了吧。
转移方程：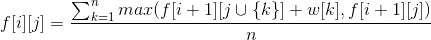
，
其中如果取不了物品k，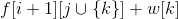
用 0 代替。
时间复杂度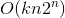
，虽然复杂度有5亿然而却跑得飞快。
#include <cstdio> #include <algorithm> #include <cstring> #define MS 17 #define MN 35005 using namespace std; int ys[MS],w[MS],prt[MS]; double f[2][MN]; int m,n,stp; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } int main() { register int i,j,k,x,lg,rg; m=read(); n=read(); for (ys[1]=1,i=2;i<=n;++i) ys[i]=ys[i-1]<<1; stp=ys[n]<<1; for (i=1;i<=n;++i) for (w[i]=read(),x=read();x;x=read()) prt[i]|=ys[x]; for (i=m-1,lg=0,rg=1;i>=0;--i,swap(lg,rg)) for (j=0;j<stp;f[lg][j++]/=n) for (f[lg][j]=0,k=1;k<=n;++k) f[lg][j]+=max(((j&prt[k])==prt[k])?f[rg][j|ys[k]]+w[k]:0,f[rg][j]); printf("%.6lf",f[rg][0]); }
Last Word
自己手算一些小数据也是不错的调试技巧。
为了缩行可能代码画风会有点崩坏。