二维询问转化成一维询问的问题,话说CF上面的好题还真多。
Description
给定一个半径为r的半圆,圆心为坐标原点O,直径为AB,半圆弧位于x轴上方。给定n次操作,每次为以下3种操作之一:
①1 x y — 在(x,y)处放置一颗卫星,如果该卫星是第 i 个被放到平面上的卫星,则它的编号为i;
②2 i — 移除编号为 i 的卫星;
③3 i j — 对卫星 i 和卫星 j 进行询问,若在卫星 i 和卫星 j 的公共控制区域能够找到一个点,满足这个点不被其他卫星所控制,那么输出"YES",否则输出"NO"。
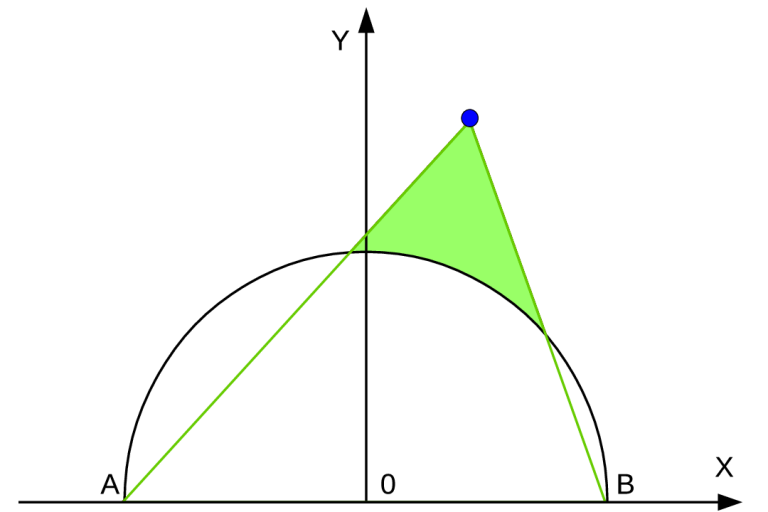
一颗卫星点P的控制区域为△PAB中的不在⊙O内的部分。如下图绿色区域:
Input
第一行两个整数r,n。
接下来n行,每行表示一个操作。
Output
对于每个操作3,输出"YES"或“NO”。
Sample Input
5 8
1 -5 8
1 -4 8
1 -3 8
1 2 7
3 1 3
2 2
3 1 3
3 3 4
Sample Output
NO
YES
YES
HINT
1<=r<=10^9,1<=n<=5*10^5。
|x|<=10^9,0<y<=10^9,且(x,y)保证在圆外。
对于操作2、3中的i、j,满足在执行此操作之前,卫星 i 和卫星 j 一定在平面上。
Solution
又是这样一道带操作的题,在开始打数据结构之前,我们分析一下题意:
操作1和操作2分别是插入和删除操作,而操作3是在询问两个二维平面的交 内是否有不被其他区间覆盖的点。
很显然就是叫我们求如下图的绿色区域内是否有其他卫星。
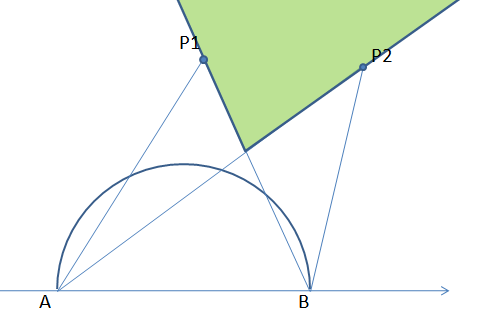
那么绿色区域内的卫星P满足什么条件呢?用k(α)表示直线α与x轴正方向的夹角,那么有:
k(AP)>k(AP2)且k(BP)<k(BP1)。
这么一来,做法一下子就变得显而易见了。
对于每个点Pi,把k(BPi)看作第一维,把k(APi)看作第二维,维护第二维出现的次数,目的是求和,判定条件是 和是否大于0。
然而数据范围是50W,如果你头戴金刚钻是可以用cdq分治O(nlog2n)通过该题的。
我们继续分析这道题的性质:我们发现两维的询问都是在询问整段序列的一半,而且判定条件是和大于1即可。
所以我们只要对于每个第一维,维护第二维的最大值,这样就变成了求矩形最大值,判定条件是 求得的最大值是否超过限制(你懂的)。
而且这个矩形最大值实际上只跟第一维有关系,询问的是第二维的全部,所以我们用线段树套堆就可以将复杂度降为O(nlogn)。
具体做法什么的只要脑补一下就行了。
最需要注意的是这题可能会带来精度上的困扰,所以各种计算和判定尽量使用向量来进行。
#include <cstdio> #include <algorithm> #include <cstring> #include <queue> #define ll long long #define l(a) (a<<1) #define r(a) (a<<1|1) #define MN 500005 #define MD 1100005 using namespace std; struct vec { int x,y; friend ll operator/(const vec& a,const vec& b) {return 1LL*a.x*b.y-1LL*a.y*b.x;} friend ll operator*(const vec& a,const vec& b) {return 1LL*a.x*b.x+1LL*a.y*b.y;} }; struct meg{int g,x,y;}a[MN]; struct met{vec v;int pos;}b0[MN],b1[MN]; struct its{int x,y;}s[MN]; struct itv{vec x,y;}d[MN]; struct Que { priority_queue <int> A,B; void push(int x) {A.push(x);} void dele(int x) {B.push(x);} int top() { while (!B.empty()&&A.top()==B.top()) A.pop(),B.pop(); if (!A.empty()) return A.top(); else return 0; } }q[MN]; int m,MQ,tin,b0in,b1in,ra; int t[MD]; inline int read() { int n=0,f=1; char c=getchar(); while (c<'0' || c>'9') {if(c=='-')f=-1; c=getchar();} while (c>='0' && c<='9') {n=n*10+c-'0'; c=getchar();} return n*f; } inline void getcg(int x,int z) {for (t[x+=MQ]=z,x>>=1;x;x>>=1) t[x]=max(t[l(x)],t[r(x)]);} inline int getmax(int L,int R) { int sum=0; for (L+=MQ,R+=MQ;L<=R;L>>=1,R>>=1) { if ( L&1) sum=max(sum,t[L++]); if (~R&1) sum=max(sum,t[R--]); } return sum; } void cghp(int x,int y,int g) { int lt=q[x].top(); if (g==1) q[x].push(y); else q[x].dele(y); if (lt!=q[x].top()) getcg(x,q[x].top()); } bool check(int x,int y) { int cs1,cs2; if (s[x].x>s[y].x) cs1=x; else cs1=y; if (s[x].y<s[y].y) cs2=x; else cs2=y; if (d[cs2].y*d[cs1].x<0) return true; else return false; } bool cmp(const met& a,const met& b) {return a.v/b.v>0;} int main() { register int i,x,y; ra=read(); m=read(); for (i=1;i<=m;++i) { a[i].g=read(); if (a[i].g==1) { x=read(); y=read(); a[i].x=++tin; d[tin].x.x=x-ra; d[tin].x.y=y; d[tin].y.x=x+ra; d[tin].y.y=y; b0[++b0in]=(met){d[tin].x,tin}; b1[++b1in]=(met){d[tin].y,tin}; } else if (a[i].g==2) a[i].x=read(); else if (a[i].g==3) a[i].x=read(),a[i].y=read(); } sort(b0+1,b0+b0in+1,cmp); sort(b1+1,b1+b1in+1,cmp); b0[0].pos=b1[0].pos=s[0].x=s[0].y=0; for (i=1;i<=b0in;++i) if (i>1&&b0[i-1].v/b0[i].v==0) s[b0[i].pos].x=s[b0[i-1].pos].x; else s[b0[i].pos].x=s[b0[i-1].pos].x+1; for (i=1;i<=b1in;++i) if (i>1&&b1[i-1].v/b1[i].v==0) s[b1[i].pos].y=s[b1[i-1].pos].y; else s[b1[i].pos].y=s[b1[i-1].pos].y+1; b0in=s[b0[b0in].pos].x; for (MQ=1;MQ<b0in;MQ<<=1); --MQ; for (i=1;i<=m;++i) { if (a[i].g<3) cghp(s[a[i].x].x,s[a[i].x].y,a[i].g); else if (a[i].g==3) { if (check(a[i].x,a[i].y)) {puts("NO"); continue;} x=max(s[a[i].x].x,s[a[i].y].x); y=min(s[a[i].x].y,s[a[i].y].y); cghp(s[a[i].x].x,s[a[i].x].y,2); cghp(s[a[i].y].x,s[a[i].y].y,2); if (getmax(1,x)>=y) puts("NO"); else puts("YES"); cghp(s[a[i].x].x,s[a[i].x].y,1); cghp(s[a[i].y].x,s[a[i].y].y,1); } } }
Last Word
又一次感受到了精度在某些题使人发狂程度的能力。
然后就不得不感叹一句向量真是好用。