题目链接:http://vjudge.net/problem/HDU-1163
题意是求N的N次方这个数字各个数位上的数相加,得到一个数,反复步骤直至这个数只剩个位。
下面证明:一个数的数根(digital root)就是它对9的余数。
引用自维基百科Digital root
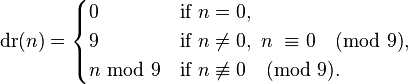
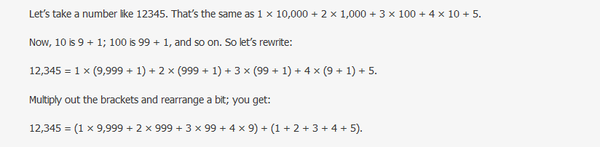
需要利用构造法证明,
令1+2+3+4+5 = y
则dr(12345) = dr(y) = dr(9n+y)
也就是说dr(y) = dr(9n+y)
令9n+y=X,则
dr(X) = dr(X%9)
X%9为个位数,所以dr(X%9) = X%9
所以dr(X) = X%9
也有特殊情况,如果X为9的倍数,那么在dr(12345) = dr(y) = dr(9n+y)中,y为9的倍数,则由dr(y) = dr(9n+y)得到dr(X) = dr(X%9)是不成立的。所以最后的结果也不成立,所以n为9的倍数的时候是特殊情况。至于为什么dr(9n)=9,可以利用上面类似的思路证明。
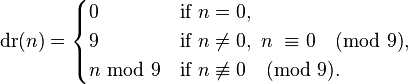
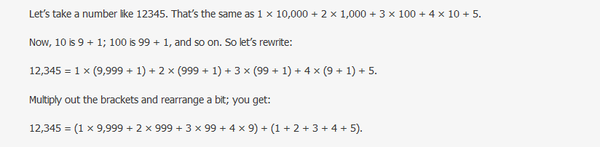
需要利用构造法证明,
令1+2+3+4+5 = y
则dr(12345) = dr(y) = dr(9n+y)
也就是说dr(y) = dr(9n+y)
令9n+y=X,则
dr(X) = dr(X%9)
X%9为个位数,所以dr(X%9) = X%9
所以dr(X) = X%9
也有特殊情况,如果X为9的倍数,那么在dr(12345) = dr(y) = dr(9n+y)中,y为9的倍数,则由dr(y) = dr(9n+y)得到dr(X) = dr(X%9)是不成立的。所以最后的结果也不成立,所以n为9的倍数的时候是特殊情况。至于为什么dr(9n)=9,可以利用上面类似的思路证明。
所以我们要求N*N*N....*N mod 9
对应(N mod9)*(N mod9)*(N mod9)...*(N mod9)
1 #include <iostream> 2 #include <cstdio> 3 #include <algorithm> 4 5 using namespace std; 6 7 int main() 8 { 9 int n,i,ans; 10 while(~scanf("%d",&n)&&n) 11 { 12 ans=n%9; 13 for(i=2;i<=n;i++) 14 { 15 ans=(ans*n)%9; 16 } 17 if(ans) printf("%d ",ans); 18 else printf("9 "); 19 } 20 return 0; 21 }