161D. Distance in Tree (树形DP)
题意:给一棵树,找两点距离为K的节点对个数
题解:
(dp[i][j]) 表示 i 节点子树距离 i 为 k 的节点个数。DP转移为:
[dp[u][0] = 1 \
dp[u][j] = sum_{v为u子节点} dp[v][j - 1] (j > 0)
]
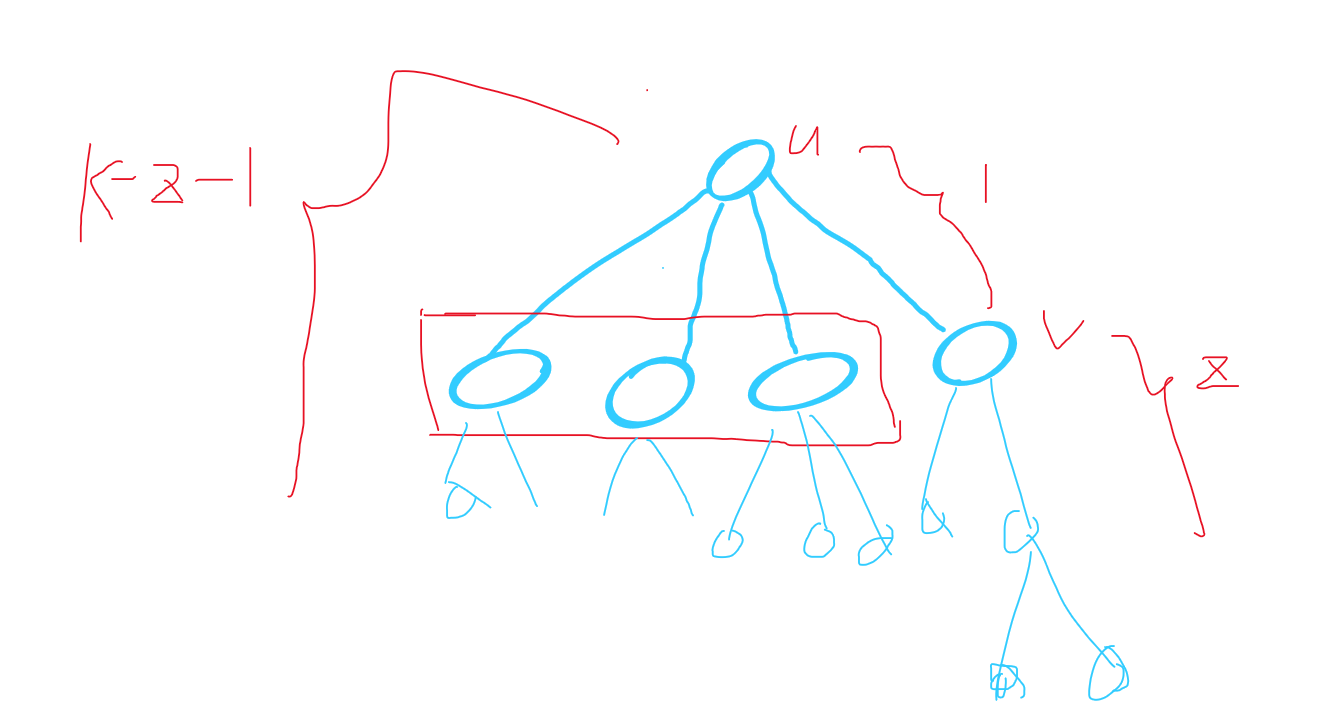
这样对每个节点 u,, 如果当前处理到子节点v, 那么此时 (dp[u][j]) 保存 v 左边兄第的和。然后假设v这边贡献 z 长度,那么找左边兄弟中的结点去凑 k 。所以:
[res = sum_{u} sum_{v是u子节点} dp[v][z] * dp[u][k - z - 1]
]
#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<queue>
#include<vector>
#include<string>
#include<fstream>
using namespace std;
#define rep(i, a, n) for(int i = a; i <= n; ++ i);
#define per(i, a, n) for(int i = n; i >= a; -- i);
typedef long long ll;
const int N = 5e4 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const ll INF = 1e9;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b & 1) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
bool cmp(int a, int b){return a > b;}
//
int n, m, k;
int head[N], cnt = 0;
int nxt[N << 1], to[N << 1];
ll dp[N][515];
ll res = 0;
void add(int u, int v){
to[cnt] = v, nxt[cnt] = head[u], head[u] = cnt ++;
to[cnt] = u, nxt[cnt] = head[v], head[v] = cnt ++;
}
void dfs(int u, int pre){
dp[u][0] = 1;
for(int i = head[u]; i != -1; i = nxt[i]){
int v = to[i];
if(v == pre) continue;
dfs(v, u);
for(int z = 0; z < k; ++ z){
res += dp[v][z] * dp[u][k - z - 1];
}
for(int z = 1; z <= k; ++ z){
dp[u][z] += dp[v][z - 1];
}
}
}
int main()
{
scanf("%d%d",&n,&k);
cnt = 0;
for(int i = 0; i <= n; ++ i) head[i] = -1;
for(int i = 1; i < n; ++ i){
int x, y; scanf("%d%d",&x,&y);
add(x, y);
}
memset(dp, 0, sizeof(dp));
dfs(1, 0);
printf("%lld
",res);
return 0;
}