Codeforces 1334D

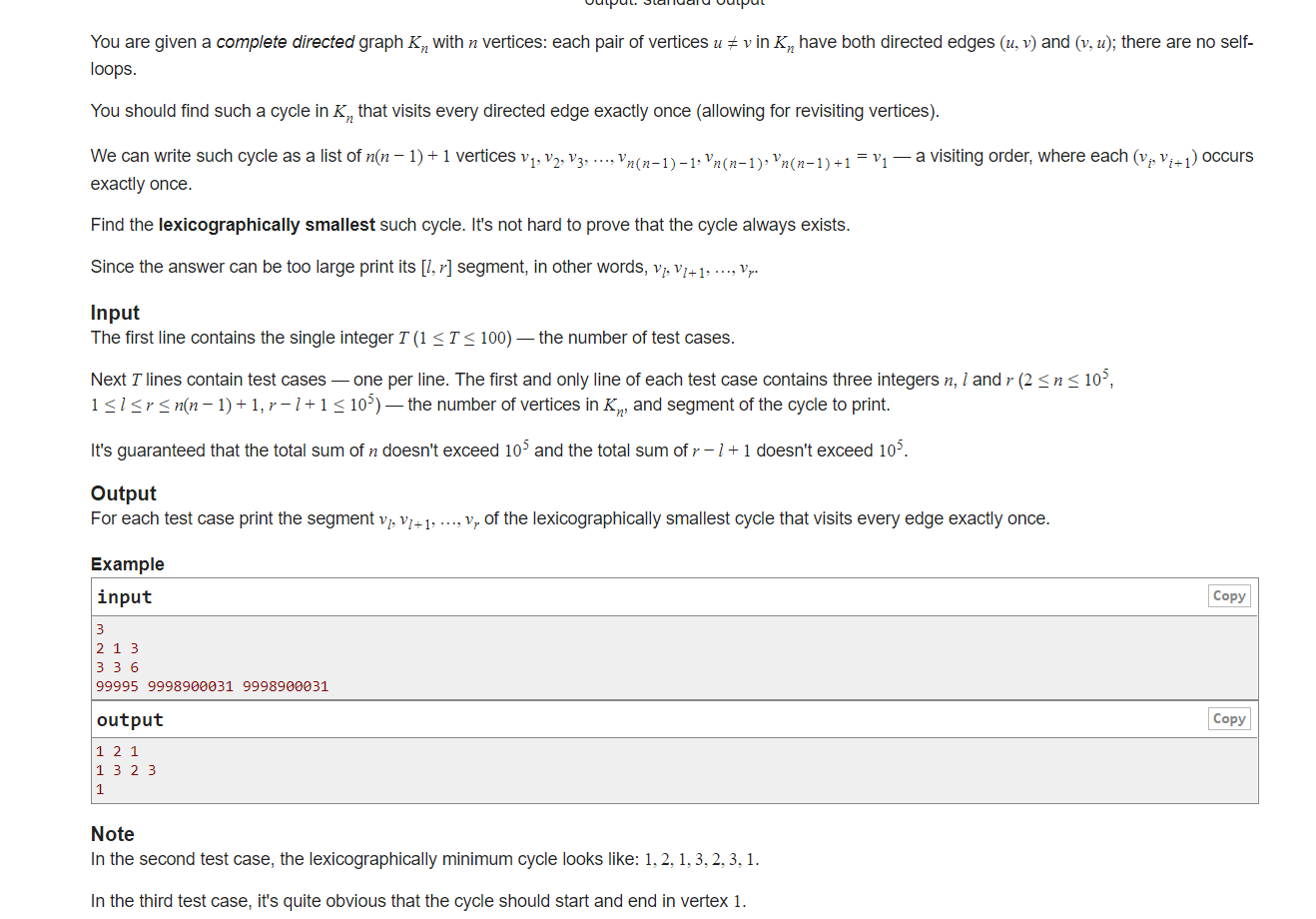
• 题意： 一个完全联通的有向图，要经过每一条边一次，访问路径由经过的节点组成，节点可以经过多次。输出“字典序最小的”路径中l,r之间的节点值。
• 题解： 要相信这类题一定有什么规律，且规律无论n的大小都满足。所以要先从n较小的情况下总结规律。本题就是最小路径类似 (以n=4为例)"1 2 1 3 1 4 2 3 2 4 3 4 1".

#include<iostream>
#include<cstdio>
#include<cstring>
#include<algorithm>
#include<cmath>
#include<map>
#include<queue>
#include<vector>
#include<string>
#include<fstream>
using namespace std;
#define rep(i, a, n) for(ll i = a; i <= n; ++ i)
#define per(i, a, n) for(ll i = n; i >= a; -- i)
typedef long long ll;
const int N = 3e6 + 105;
const int mod = 998244353;
const double Pi = acos(- 1.0);
const int INF = 0x3f3f3f3f;
const int G = 3, Gi = 332748118;
ll qpow(ll a, ll b) { ll res = 1; while(b){ if(b) res = (res * a) % mod; a = (a * a) % mod; b >>= 1;} return res; }
ll gcd(ll a, ll b) { return b ? gcd(b, a % b) : a; }
//

ll T, l, r, n;
ll sum[N];

void print(ll base,ll st, ll et){
    rep(i,st,et){
        if(i & 1) printf("%lld ",base);
        else printf("%lld ", i / 2 + base);
    }
}

int main()
{
    scanf("%lld",&T);
    while(T --){
        scanf("%lld%lld%lld",&n,&l,&r);
        ll flag = 0;
        sum[0] = 0;
        rep(i,1,n - 1)
            sum[i] = sum[i - 1] + 2ll * (n - i);
        
        if(r > sum[n - 1]){
            flag = 1;
            if(l == r){
                printf("1
");
                continue;
            }
            r --;
        }
        ll lt = 0, rt = 0;
        rep(i,1,n){
            if(sum[i] >= l && !lt) lt = i;
            if(sum[i] >= r && !rt) rt = i;
        }
        l = l - sum[lt - 1];
        r = r - sum[rt - 1];
        if(lt == rt){
            print(lt,l,r);
        }
        else{
            print(lt, l, 2ll * (n - lt));
            ll top = lt + 1;
            while(top < rt){
                print(top,1,2ll * (n - top));
                top ++;
            }
            print(rt,1ll,r);
        }
        if(!flag) printf("
");
        else printf("1
");
    }
    return 0;
}