T1
三个操作实际上是两个
1.把x -1
2.把x *k
而100000的ans也不过是50步,因为是指数增长
设 f[i] 为走到i这个值用到的最少步数
那可以枚举步数,然后来更新它能走到的位置

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#define mem(a,b) memset(a,b,sizeof(a))
#define ll long long
using namespace std;
const int N=1000006;
int n;
int f[N*10];
int main(){
scanf("%d",&n);
mem(f,-1);
f[1]=0;
int step=0;
while(f[n]==-1)
{
++step;
for(int i=0;i<=n+50;++i)
if(f[i]!=-1)
{
if(f[i*(step-f[i])]==-1)
f[i*(step-f[i])]=step;
if(i>0)
{
if(f[i-1]==-1)
f[i-1]=f[i]+1;
else
if(f[i-1]>f[i]+1)
f[i-1]=f[i]+1;
}
}
}
cout<<f[n];
}
T2
不知道正解是什么
他们从网上找了一篇17page的英文论文,我表示看不懂
然后 正哥打了杜教筛,O(n^(1/3)),正解好象是O(n^(0.4))...
ans=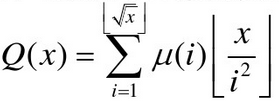
x/(i*i)可以分块,然后就转化成了求mu的前缀和
要求前缀和范围是1e9,但是只能预处理7e7...
所以要用杜教筛...(好,联赛水题)
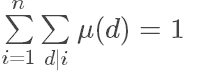 ............(1)
............(1)
这个就是莫比乌斯反演那个东西
只有当i==1的时候,才会==1
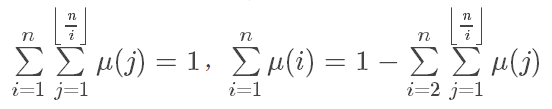 ..........(2)
..........(2)
这个证明的话
(1)式,i=d*T,d是因数,T是倍数
(2)式,就变成 枚举倍数,实际上是一样的
然后(2)式 是递归形式,可以递归求,而且(2)式也可以分块求
然后就可以在O(n^(1/3))计算出来了

#include <cstdio>
#include <cstring>
#include <cstdlib>
#include <iostream>
#include <cmath>
#include <algorithm>
#define ll long long
#define dd double
#define mem(a,b) memset(a,b,sizeof(a))
using namespace std;
const int N=70000006;
const int mod=76543;
int prime[2433706],cnt;
bool he[N];
int mu[N];
void chu()
{
mu[1]=1;
for(int i=2;i<N;++i)
{
if(!he[i])
{
prime[++cnt]=i;
mu[i]=-1;
}
for(int j=1;j<=cnt&&(ll)prime[j]*i<N;++j)
{
he[i*prime[j]]=1;
if(i%prime[j]==0)
{
mu[i*prime[j]]=0;
break;
}
mu[i*prime[j]]=-mu[i];
}
}
for(int i=1;i<N;++i)
mu[i]+=mu[i-1];
}
ll n;
struct son
{
ll u,v;
int next;
}a1[N/10];
int first[mod],e,ttt;
inline void addbian(ll u,ll v)
{
ttt=u%mod;
a1[e].v=v;
a1[e].u=u;
a1[e].next=first[ttt];
first[ttt]=e++;
}
ll presum(ll x)
{
if(x<N)
return mu[x];
int kkk=x%mod;
for(int i=first[kkk];i!=-1;i=a1[i].next)
if(a1[i].u==x)
return a1[i].v;
ll nx,ans=1;
for(ll i=2;i<=x;)
{
nx=x/(x/i);
ans-=(nx-i+1)*presum(x/i);
i=nx+1;
}
addbian(x,ans);
return ans;
}
ll get(ll s,ll t)
{
return presum(t)-presum(s-1);
}
int main(){
mem(first,-1);
chu();
scanf("%lld",&n);
ll q1=sqrt((dd)n),nx,ans=0;
for(ll i=1;i<=q1;)
{
nx=sqrt( n/(n/(i*i)) );
ans+=(n/(i*i))*get(i,nx);
i=nx+1;
}
cout<<ans;
}
T3
模拟Treap可以60分
正解是 线段树
首先把询问全都离线下来,离散一下
按照k为下标W为权值建线段树
由于是大根堆,ku和kv的lca其实就是[ku,kv]区间w最大的那个值(这个其实可以想想Treap的建树过程)
然后问题就只剩下 求ku,kv,lca到根节点的距离d了
d=pos向左向右的最长上升序列 (pos节点的父亲节点的w一定比它大)
这个 最长上升序列长度 就可以用线段树维护,这跟bzoj2957楼房重建一样了

#include <cstdio>
#include <cstring>
#include <iostream>
#include <algorithm>
#include <cstdlib>
#define mem(a,b) memset(a,b,sizeof(a))
#define ll long long
using namespace std;
const int N=200006;
struct Q
{
int op;
ll t[2];
}q[N];
struct LI
{
int pos,ff;
ll val;
bool friend operator < (LI a,LI b)
{
return a.val<b.val;
}
}li[N*2];
int con;
ll val[N*4];
int dui[N*4];
struct TREE
{
ll mx[N*8];
int cnt[N*8];
int cal(ll c,int l,int r,int x)
{
if(l==r)
return mx[x]>c;
int mid=(l+r)>>1;
if(mx[x<<1]<=c)
return cal(c,mid+1,r,x<<1|1);
return cal(c,l,mid,x<<1)+cnt[x]-cnt[x<<1];
}
inline void pushup(int l,int r,int x)
{
int mid=(l+r)>>1;
mx[x]=(mx[x<<1]>mx[x<<1|1]?mx[x<<1]:mx[x<<1|1]);
cnt[x]=cnt[x<<1]+cal(mx[x<<1],mid+1,r,x<<1|1);
}
void add(int pos,ll c,int l,int r,int x)
{
if(l==r)
{
mx[x]=c;cnt[x]=1;
return ;
}
int mid=(l+r)>>1;
if(pos<=mid)
add(pos,c,l,mid,x<<1);
else
add(pos,c,mid+1,r,x<<1|1);
pushup(l,r,x);
}
ll qqmax(int L,int R,int l,int r,int x)
{
if(L<=l&&r<=R)
return mx[x];
int mid=(l+r)>>1;
ll ans=0;
if(L<=mid)
ans=max(ans,qqmax(L,R,l,mid,x<<1));
if(mid<R)
ans=max(ans,qqmax(L,R,mid+1,r,x<<1|1));
return ans;
}
int qq(int L,int R,int l,int r,int x)
{
//printf("Tsh L=%d R=%d l=%d r=%d x=%d
",L,R,l,r,x);
if(L<=l&&r<=R)
return cnt[x];
int mid=(l+r)>>1,ans=0;
if(R<=mid)
return qq(L,R,l,mid,x<<1);
if(mid<L)
return qq(L,R,mid+1,r,x<<1|1);
return qq(L,mid,l,mid,x<<1)+cal(qqmax(L,R,l,mid,x<<1),mid+1,r,x<<1|1);
}
}Tsh;
struct TREe
{
ll mx[N*8];
int cnt[N*8];
int cal(ll c,int l,int r,int x)
{
if(l==r)
return mx[x]>c;
int mid=(l+r)>>1;
if(mx[x<<1|1]<=c)
return cal(c,l,mid,x<<1);
return cal(c,mid+1,r,x<<1|1)+cnt[x]-cnt[x<<1|1];
}
inline void pushup(int l,int r,int x)
{
int mid=(l+r)>>1;
mx[x]=(mx[x<<1]>mx[x<<1|1]?mx[x<<1]:mx[x<<1|1]);
cnt[x]=cnt[x<<1|1]+cal(mx[x<<1|1],l,mid,x<<1);
}
void add(int pos,ll c,int l,int r,int x)
{
if(l==r)
{
mx[x]=c;cnt[x]=1;
return ;
}
int mid=(l+r)>>1;
if(pos<=mid)
add(pos,c,l,mid,x<<1);
else
add(pos,c,mid+1,r,x<<1|1);
pushup(l,r,x);
}
ll qqmax(int L,int R,int l,int r,int x)
{
if(L<=l&&r<=R)
return mx[x];
int mid=(l+r)>>1;
ll ans=0;
if(L<=mid)
ans=max(ans,qqmax(L,R,l,mid,x<<1));
if(mid<R)
ans=max(ans,qqmax(L,R,mid+1,r,x<<1|1));
return ans;
}
int qq(int L,int R,int l,int r,int x)
{
//printf("Txi L=%d R=%d l=%d r=%d x=%d
",L,R,l,r,x);
if(L<=l&&r<=R)
return cnt[x];
int mid=(l+r)>>1,ans=0;
if(R<=mid)
return qq(L,R,l,mid,x<<1);
if(mid<L)
return qq(L,R,mid+1,r,x<<1|1);
return qq(L,R,mid+1,r,x<<1|1)+cal(qqmax(L,R,mid+1,r,x<<1|1),l,mid,x<<1);
}
}Txi;
int n,mm;
int get(int pos)
{
//printf("pos=%d
",pos);
return Tsh.qq(pos,mm,1,mm,1)+Txi.qq(1,pos,1,mm,1);
}
void lisan()
{
for(int i=1;i<=n;++i)
{
if(q[i].op==0)
li[++con]=(LI){i,0,q[i].t[0]};
else
if(q[i].op==1)
li[++con]=(LI){i,0,q[i].t[0]};
else
{
li[++con]=(LI){i,0,q[i].t[0]};
li[++con]=(LI){i,1,q[i].t[1]};
}
}
sort(li+1,li+1+con);
li[0].val=-111;mm=0;
for(int i=1;i<=con;++i)
{
if( li[i].val==li[i-1].val )
q[li[i].pos].t[li[i].ff]=mm;
else
q[li[i].pos].t[li[i].ff]=++mm;
}
con=0;
for(int i=1;i<=n;++i)
if(q[i].op==0)
li[++con]=(LI){i,1,q[i].t[1]};
sort(li+1,li+1+con);
for(int i=1;i<=con;++i)
{
q[li[i].pos].t[li[i].ff]=i;
dui[i]=q[li[i].pos].t[0];
}
}
int main(){
//freopen("T3.in","r",stdin);
scanf("%d",&n);
for(int i=1;i<=n;++i)
{
scanf("%d",&q[i].op);
if(q[i].op==0)
scanf("%lld%lld",&q[i].t[0],&q[i].t[1]);
else
if(q[i].op==1)
scanf("%lld",&q[i].t[0]);
else
scanf("%lld%lld",&q[i].t[0],&q[i].t[1]);
}
lisan();
/*printf("
");
for(int i=1;i<=n;++i)
printf("hhh %d %lld %lld
",q[i].op,q[i].t[0],q[i].t[1]);
printf("
");*/
for(int i=1;i<=n;++i)
{
if(q[i].op==0)
{
Tsh.add(q[i].t[0],q[i].t[1],1,mm,1);
Txi.add(q[i].t[0],q[i].t[1],1,mm,1);
val[q[i].t[0]]=q[i].t[1];
}
else
if(q[i].op==1)
{
Tsh.add(q[i].t[0],-val[q[i].t[0]],1,mm,1);
Txi.add(q[i].t[0],-val[q[i].t[0]],1,mm,1);
}
else
{
int lca;
if(q[i].t[0]<=q[i].t[1])
lca=dui[Tsh.qqmax(q[i].t[0],q[i].t[1],1,mm,1)];
else
lca=dui[Tsh.qqmax(q[i].t[1],q[i].t[0],1,mm,1)];
//printf("lca=%d
",lca);
printf("%d
",get(q[i].t[0])+get(q[i].t[1])-2*get(lca) );//printf("i=%d
",i);
}
}
}
昨天这个题我感觉极其难,反正考试全都打了暴力...
但是 做难事必有所得 --------某建老师
做难题才有提升...
