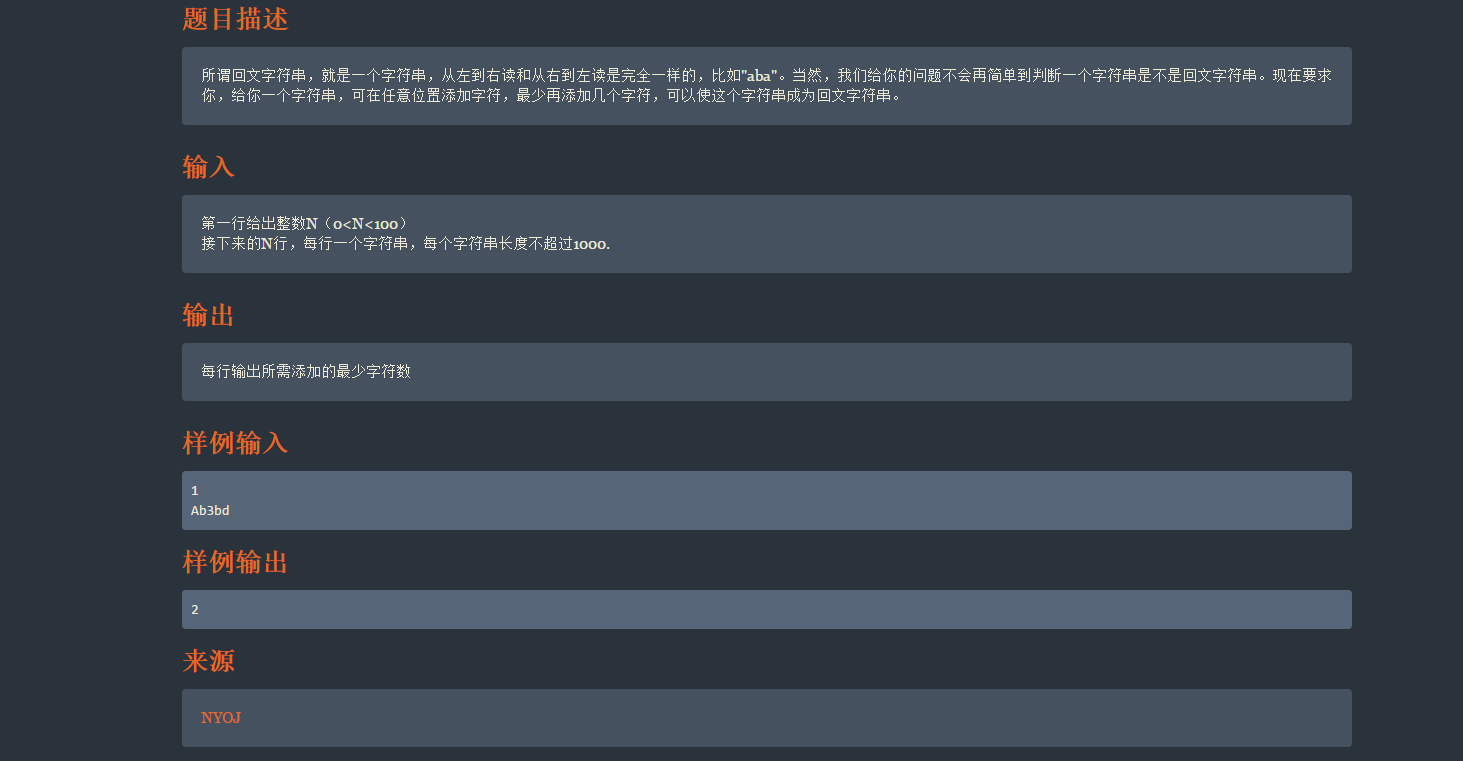
和那个 括号匹配 , 郑轻的比赛项链 , 和 普通的括号匹配 差不多 , 明天需要把这些做一下 , 然后总结一下
1 #include<stdio.h>
2 #include<string.h>
3 #include<math.h>
4 #include<iostream>
5 #include<algorithm>
6 #include<queue>
7 #include<vector>
8 #include<set>
9 #include<stack>
10 #include<string>
11 #include<sstream>
12 #include<map>
13 #include<cctype>
14 #include<limits.h>
15 using namespace std; // 类似于 括号匹配 . 但是还是有 不少区别的 .
16 int t,l,dp[1005][1005];
17 int main()
18 {
19 char a[1005];
20 scanf("%d",&t);
21 while(t--)
22 {
23 scanf("%s",a+1); // 这样 就从 第一个 开始了
24 l=strlen(a+1);
25 for(int i=0;i<=l;i++)
26 dp[i][i]=dp[i][i-1]=0;
27 for(int q=1;q<l;q++)
28 {
29 for(int i=1;i<=l-q;i++)
30 {
31 int j=i+q;
32 dp[i][j]=10000;
33 if(a[i]==a[j])
34 dp[i][j]=dp[i+1][j-1];
35 dp[i][j]=min(dp[i][j],dp[i+1][j]+1);
36 dp[i][j]=min(dp[i][j],dp[i][j-1]+1);
37 }
38 }
39 printf("%d
",dp[1][l]);
40 }
41 return 0;
42 }
上述是一种经典的解法 , 但是暂时想不出来应该怎么弄出来 , 回文串 , 可以和最长公共子串联系起来 . 第一种是 , 经典的正规军 , 高效专业 , 第二种就是 举一反三了 . 效率不是太高 .
1 #include<stdio.h>
2 #include<string.h>
3 #include<math.h>
4 #include<iostream>
5 #include<algorithm>
6 #include<queue>
7 #include<vector>
8 #include<set>
9 #include<stack>
10 #include<string>
11 #include<sstream>
12 #include<map>
13 #include<cctype>
14 #include<limits.h>
15 using namespace std;
16 char a[2222],b[2222];
17 int c[500][500];
18 int main()
19 {
20 int i=0,j=0,a1,b1,t;
21 scanf("%d",&t);
22 while(t--)
23 {
24 scanf("%s",a);
25 a1=strlen(a);
26 for(int i=0;i<a1;i++)
27 b[i]=a[a1-i-1];
28 memset(c,0,sizeof(c));
29 for(i=1;i<=a1;i++)
30 {
31 for(j=1;j<=a1;j++)
32 {
33 if(a[i-1]==b[j-1])
34 c[i][j]=c[i-1][j-1]+1; // 相等的话 取 右上角
35 else
36 c[i][j]=max(c[i-1][j],c[i][j-1]); // 不相等 的话 在 左边或上边 取一个最大的
37 }
38 }
39 printf("%d
",c[a1][b1]);
40 }
41 return 0;
42 }
把上面说的 几种题型再过一遍 , 可能就对那个 动态规划的 核心代码有了一定的了解 .
