什么是堆?
优先队列(Priority Queue):特殊的“队列”,取出元素的顺序是依照元素的优先级(关键字)大小,而不是元素进入队列的先后顺序。
下面再次开始储存选择 ::>_<::

堆堆堆,完全二叉树。。用数组表示。。o(∩_∩)o 哈哈。。。我仿佛又燃烧了起来!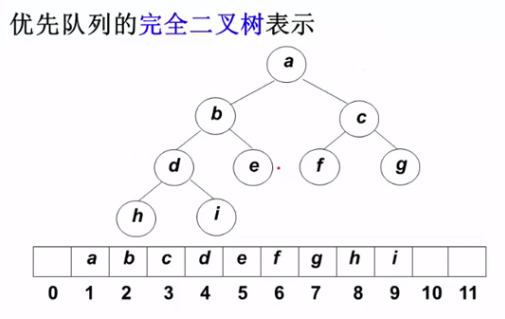
→堆得两个特性
结构性:用数组表示的完全二叉树:
有序性:任一节点的关键字使其子树所有节点的最大值(最小值)
♢“最大堆(MaxHeap)”也称“大顶堆”;最大值
♢“最小堆(MinHeap)”也称“小顶堆”;最小值

1:完全二叉树。2:有序性。
数据对象集:完全二叉树,每个节点的元素值不小于其子节点的元素值 操作集: 最大堆H∈MaxHeap 元素item∈ElementType,主要操作有; ------MaxHeap Create(int MaxSize):创建一个空的最大堆 ------Boolean IsFull(MaxHeap H):判断最大堆H是否已满 ------Insert (MaxHeap H,ElementType item):将元素item插入最大堆H。 ------Boolean IsEmpty(MaxHeap H):判断最大堆H是否为 MaxHeap Create(int MaxSize) {//创建容量为MaxSize的空的最大堆。 MaxHeap H=malloc(sizeof(struct HeapStruct)); H->Elements=malloc((MaxSize+1)*sizeof(ElementType)); H->Size=0; //堆的当前元素个数 为0 //现在才开始创建堆 H->CapaCity=MaxSize; //用于记忆堆的最大容量是多少(MaxSize)。 H->Elements[0]=MaxDate;//哨兵 为最大堆中所有元素的可能的值,便于以后更快的操作。 return H; }
void Insert (MaxHeap H,ElementType item)//在堆
ElementType DeleteMax(MaxHeap H) { //从最大堆H中取出关键值为最大的元素,并且删除一个节点. int Parent,Child; ElementType MaxItem,Temp; if(IsEmpty(H)) { printf("最大堆为空 "); return ; } MaxItem=H->Element[1];// 把最大的元素先储存起来,用于返回. temp=H->Elements[H->Size--];//本来元素个数就需要减一,所以这样一起搞定,让temp=最后的元素, for(Paren=1;Parent*2<=H->Size;Parent=Child) { Child=2*Parent; if((Child!=H->Size)&&(H->Elements[Child])<H->Elements[Child+1]) Child++; if(temp>=H->Elements[Child]) break; else H->Elements[Parent]=H->Elements[Child]; } H->Elements[Parent]=temp; return MaxItem; }
H中插入 item { //将元素iten插入最大堆H,其中H->Elements[0]已经定义为哨兵 int i; if(IsFull(H)) { printf("最大堆已满 "); return ; } i=++H->Size;//将堆中的元素扩大了一。 for(;H->Elements[i/2]<item;i/=2) //将需要插入元素和气所在位置的祖上比较 H->Elements[i]=H->Elements[i/2]; H->Elements[i]=item; }
ElementType DeleteMax(MaxHeap H) { //从最大堆H中取出关键值为最大的元素,并且删除一个节点. int Parent,Child; ElementType MaxItem,Temp; if(IsEmpty(H)) { printf("最大堆为空 "); return ; } MaxItem=H->Element[1];// 把最大的元素先储存起来,用于返回. temp=H->Elements[H->Size--];//本来元素个数就需要减一,所以这样一起搞定,让temp=最后的元素, for(Paren=1;Parent*2<=H->Size;Parent=Child) { Child=2*Parent; if((Child!=H->Size)&&(H->Elements[Child])<H->Elements[Child+1]) Child++; if(temp>=H->Elements[Child]) break; else H->Elements[Parent]=H->Elements[Child]; } H->Elements[Parent]=temp; return MaxItem; }
/*最大堆的建立*/
将已存在的N个元素按照最大堆的要求放在一个一维数组中
方法1:通过插入操作,将N个元素一个一个相继的插入到一个初始为空的堆中去.时间最大代价为NlogN