背包问题
01背包
每个物品选择一次,选或者不选
dp[i][j] 表示从下标为[0-i]的物品里任意取,放进容量为j的背包,价值总和最大是多少。
dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]); //背包容量是减少的
- 二维初始化
因为是从i-1转换来的,所以初始化i=0的情况
// 倒叙遍历 正序则第一个重复放置
for (int j = bagWeight; j >= weight[0]; j--) {
dp[0][j] = dp[0][j - weight[0]] + value[0]; // 初始化i为0时候的情况
}
- 转换一维
dp[j]表示:容量为j的背包,所背的物品价值可以最大为dp[j],那么dp[0]就应该是0,因为背包容量为0所背的物品的最大价值就是0。
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
//顺序不可颠倒,先物品后容量,并且容量倒叙
for(int i = 0; i < weight.size(); i++) { // 遍历物品
for(int j = bagWeight; j >= weight[i]; j--) { // 遍历背包容量
dp[j] = max(dp[j], dp[j - weight[i]] + value[i]);
}
}
完全背包
每个物品可以多次选取
字符串问题
lt1143 最长公共子序列(长度)
dp[i][j]
int longestCommonSubsequence(string text1, string text2) {
int m = text1.size();
int n = text2.size();
int dp[m+1][n+1];
memset(dp,0,sizeof(dp));
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
if(text1[i-1]==text2[j-1])
{
dp[i][j] = dp[i-1][j-1]+1;
}
else{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
return dp[m][n];
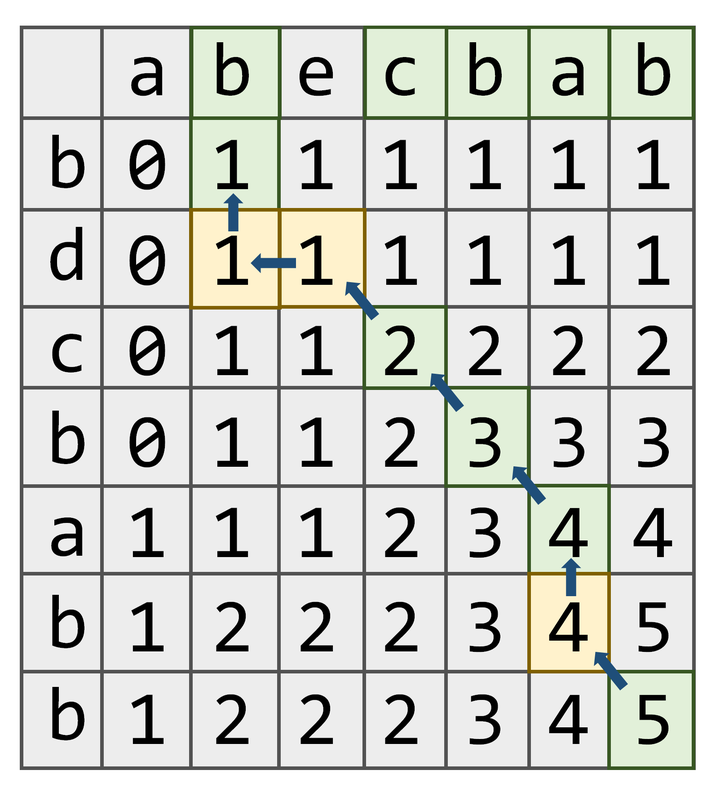
牛客 最长公共子序列(具体序列)
得到dp数组后,从后向前推导
string LCS(string s1, string s2) {
// write code here
//不符合条件返回-1
if(s1.size()==0||s2.size()==0) return "-1";
int m = s1.size();
int n = s2.size();
string res = "";
int dp[m+1][n+1];
memset(dp,0,sizeof(dp));
for(int i=1;i<=m;i++)
for(int j= 1;j<=n;j++)
{
if(s1[i-1]==s2[j-1])
dp[i][j] = dp[i-1][j-1]+1;
else
{
dp[i][j] = max(dp[i-1][j],dp[i][j-1]);
}
}
//没有公共子序列 返回"-1"
if(dp[m][n]==0) return "-1";
while(dp[m][n])
{
if(dp[m-1][n]==dp[m][n-1]&&dp[m][n]>dp[m-1][n-1])
{
res+=s1[m-1];
//res.push_back(s1[m-1]);
m--;
n--;
}
else if(dp[m-1][n]>dp[m][n-1])
m--;
else{
n--;
}
}
reverse(res.begin(),res.end());
return res;
}
牛客 最长公共子串(具体序列)
子串是连续的,判断简单,找到最长和i或者j位置,反推
string LCS(string str1, string str2) {
// write code here
//保留最长子串的值和位置
int m = str1.size();
int n = str2.size();
if(m==0||n==0)return "-1";
int dp[m+1][n+1];
memset(dp,0,sizeof(dp));
int len = 0,end = 0;
for(int i=1;i<=m;i++)
for(int j=1;j<=n;j++)
{
if(str1[i-1]==str2[j-1])
{
dp[i][j] = dp[i-1][j-1]+1;
//判断是否更大
}
if(dp[i][j]>len)
{
end = i;
len = dp[i][j];
}
}
if(len==0)return "-1";
//本质end-start+1 = len 得到 start= end-len+1 因为end是下标后面一位,所以start = end-len
return str1.substr(end-len,len);
}
编辑字符串
字节二面
给定两个字符串str1和str2,再给定三个整数ic,dc和rc,分别代表插入、删除和替换一个字符的代价,请输出将str1编辑成str2的最小代价。
"abc","adc",5,3,2返回2
注意是把str1编辑成str2,开始理解错题意了
dp[i][j] 是str1前i个字符转换到str2前j个字符需要的次数
1.dp[i][j-1] 是str1前i和str2前j-1子问题,对于str2的第j个字符,str1插入一个即可,所以dp[i][j] = dp[i][j-1]+ic
2.dp[i-1][j] 是str1前i-1和str2前j子问题,对于str1的第i个字符,删除第i个,所以 dp[i][j] = dp[i-1][j]+dc
3.dp[i-1][j-1] 同理 dp[i][j] = dp[i-1][j-1]+rc
int minEditCost(string str1, string str2, int ic, int dc, int rc) {
// write code here
int m = str1.size();
int n = str2.size();
vector<vector<int>>dp(m+1,vector<int>(n+1,0));
//str1的前n个
for(int i=0;i<=m;i++)
{
dp[i][0] = i*dc;
}
for(int j=0;j<=n;j++)
{
dp[0][j] = j*ic;
}
for(int i=1;i<=m;i++)
for (int j=1;j<=n;j++)
{
//取出为i-1和j-1,因为 dp[i][j]代表i个j个,索引位置是从0开始的
char one = str1[i-1];
char two = str2[j-1];
if(one==two)
dp[i][j] = dp[i-1][j-1];
else{
//理解这部分 和j-1 匹配少一个,和j匹配多一个
int insert = dp[i][j-1]+ic;
int del = dp[i-1][j]+dc;
int replace = dp[i-1][j-1]+rc;
dp[i][j] = min(insert,min(del,replace));
}
}
return dp[m][n];
}
lt72 编辑距离
单词word1到word2 需要的最少编辑次数
int minDistance(string word1, string word2) {
int m = word1.size();
int n = word2.size();
//dp[i][j]代表word1的前i转变为word2前j需要的最少次数
vector<vector<int>>dp(m+1,vector<int>(n+1));
for(int i=0;i<=m;i++)
{
dp[i][0] = i;
}
for(int j = 0;j<=n;j++)
{
dp[0][j] = j;
}
for(int i=1;i<=m;i++)
{
for(int j=1;j<=n;j++)
{
//相等不改变
if(word1[i-1]==word2[j-1])
{
dp[i][j] = dp[i-1][j-1];
}
else{//不等取最小的
dp[i][j] = min(dp[i-1][j-1],min(dp[i-1][j],dp[i][j-1]))+1;
}
}
}
return dp[m][n];
}
offer19 正则表达匹配
.代表匹配任意字符
*代表前面字符的0次或者多次(可以和前面的字符一起消失)
bool isMatch(string s, string p) {
int m = s.size();
int n =p.size();
vector<vector<bool>>dp(m+1,vector<bool>(n+1));
for (int i=0;i<=m;i++){
for(int j=0;j<=n;j++){
//匹配串为空
if(j==0)
{
dp[i][0] = i==0;
}else{
//非空串
if(p[j-1]!='*'){
if(i>0&&(s[i-1]==p[j-1]||p[j-1]=='.'))
dp[i][j] = dp[i-1][j-1];
}else{
//去掉*和它前面的字符
if(j>=2)
dp[i][j] = dp[i][j]||dp[i][j-2];
//*前字符和i位置相等或者*前为.
if(i>0&&j>=2&&(s[i-1]==p[j-2]||p[j-2]=='.'))
dp[i][j] = dp[i][j]||dp[i-1][j];
}
}
}
}
return dp[m][n];
}
通配符匹配
? 代表任意字符
- 代表任意字符串包括空串
dp[i][j]代表s的前i和p的前j是否匹配
bool isMatch(const char *s, const char *p) {
int m = strlen(s);
int n = strlen(p);
vector<vector<bool>>dp(m+1,vector<bool>(n+1));
//特殊情况 p全是*时是可以匹配的
for(int i=1;i<=n;i++)
{
if(p[i-1]!='*')
break;
dp[0][i] = true;
}
for(int i=0;i<=m;i++)
{
for(int j=0;j<=n;j++)
{
if(j==0)
{
dp[i][j]=(i==0);
}else{
if(p[j-1]!='*')
{
if(i>0&&(p[j-1]=='?'||p[j-1]==s[i-1]))
dp[i][j] = dp[i-1][j-1];
}else{
//直接去除
if(i>=1)
dp[i][j] = dp[i][j]||dp[i-1][j]||dp[i][j-1];
}
}
}
}
return dp[m][n];
}
lt76 最小覆盖子串
输入:s = "ADOBECODEBANC", t = "ABC"
输出:"BANC"
滑动窗口 两个map分别记录t串和s中t字符出现次数
//hash t已经存在的 count 是记录过程
unordered_map<char,int>hash,count;
bool check()
{
//从已经计算好的t串hash判断count
for (unordered_map<char,int>::iterator iter = hash.begin();iter!=hash.end();iter++){
if(count[iter->first]<iter->second)
return false;
}
return true;
}
string minWindow(string s, string t) {
int m = s.size();
int n = t.size();
//t串放入hash
for(int i=0;i<n;i++)
{
hash[t[i]]++;
}
int len=INT_MAX,resL=-1,l = 0,r = -1;
while(r<m)
{
//访问的字符在hash存在则记录字符出现个数
if(hash.find(s[++r])!=hash.end())
{
count[s[r]]++;
}
//符合条件,则l移动缩短字符串长度
while(check()&&l<=r)
{
if(r-l+1<len)
{
len = r-l+1;
resL = l;
}
//向右移动时,当前字符在hash中则count数减少
if(hash.find(s[l])!=hash.end())
{
count[s[l]]--;
}
l++;
}
}
return resL==-1?"":s.substr(resL,len);
}
排列组合回溯
lt22括号生成
输入:n = 3 输出:["((()))","(()())","(())()","()(())","()()()"]
回溯,左括号数量大于右括号数量则不符合规则
vector<string>res;
string path;//全局变量
vector<string> generateParenthesis(int n) {
string path = "";
backtrack(n,n);
return res;
}
//回溯剪枝
void backtrack(int left,int right)
{
if(left>right)
return ;
if(left==0&&right==0)
{
res.push_back(path);
return ;
}
if(left>0)
{
path.push_back('(');
backtrack(left-1,right);
path.pop_back();
}
if(right>0)
{
path.push_back(')');
backtrack(left,right-1);
path.pop_back();
}
}
- 全排列问题
使用used标识是否访问过,每层从0开始不用start,可能需要对字符进行排序
两种,一种可以重复,第二种不可重复,假设abb,全排列只要一个abb,两种used标识方法不同
子集问题: 需要使用start标识层数
N皇后,每层需要start确定层数
lt46 无重复数组全排列
回溯,没有重复数组的全排列
vector<vector<int>>res;
vector<vector<int>> permute(vector<int>& nums) {
if(nums.size()==0)return {};
int m = nums.size();
vector<bool>used(m+1,false);
vector<int>path;
backtrack(nums,path,used);
return res;
}
//每次从0开始,不需要计算层数的标识start
void backtrack(vector<int>nums,vector<int>&path,vector<bool>used)
{
if(path.size()==nums.size())
{
res.push_back(path);
return ;
}
for(int i=0;i<nums.size();i++)
{
if(!used[i])
{
path.push_back(nums[i]);
used[i] = true;
backtrack(nums,path,used);
used[i] = false;
path.pop_back();
}
}
}
lt47 有重复数组全排列
有重复需要排序,并且判断是否重复
vector<vector<int>> permuteUnique(vector<int>& nums) {
//有序,判断前置,同层不计算
vector<int>path;
vector<bool>used(nums.size(),false);
sort(nums.begin(),nums.end()); //有重复需要排序
backtrack(nums,path,used);
return res;
}
//每次从0开始,不需要计算层数的标识start
void backtrack(vector<int>nums,vector<int>&path,vector<bool>used)
{
if(path.size()==nums.size())
{
res.push_back(path);
return ;
}
for(int i=0;i<nums.size();i++)
{
if(!used[i])
{
//两个重复前一个没使用则表示重复,跳过这次
if(i>0&&nums[i]==nums[i-1]&&!used[i-1])
continue;
path.push_back(nums[i]);
used[i] = true;
backtrack(nums,path,used);
used[i] = false;
path.pop_back();
}
}
}
golang版本
var res [][]int
var path []int
func permuteUnique(nums []int) [][]int {
if len(nums)==0{
return res
}
res = make([][]int,0)
path = make([]int,0)
used:=make([]bool,len(nums))
sort.Ints(nums)
dfs(nums,used)
return res
}
func dfs(nums []int, used []bool){
if len(path)==len(nums){
ret:=make([]int,len(path))
copy(ret,path)
res = append(res,ret)
return
}
for i:=0;i<len(nums);i++{
if i>0&&nums[i-1]==nums[i]&&used[i-1]==false{
continue
}
if used[i]{
continue
}
path = append(path,nums[i])
used[i] = true
dfs(nums,used)
used[i] = false
path = path[:len(path)-1]
}
}
牛客 字符串的排列
abc 所有排列方式,按照字典序
- set排序递归
时间O(n!)
set<string>hash;
vector<string> Permutation(string str) {
if(str=="")return vector<string>();
dfs(str,0);
return vector<string>(hash.begin(),hash.end());
}
void dfs(string &str,int start)
{
if(start==str.size())
{
hash.insert(str);
return ;
}
for(int i = start;i<str.size();i++)
{
swap(str[start],str[i]);
dfs(str,start+1);
swap(str[start],str[i]);
}
}
- 回溯使用used标记
每层从0开始,不可重复2需要对初始字符串排序if(i>0&&nums[i]nums[i-1]&&!used[i-1])
**子集问题判断条件为if(i>start&&nums[i]nums[i-1])**
vector<string>res;//全局记录
vector<string> Permutation(string str) {
if(str.size()==0) return {};
string path = "";
vector<bool>used(str.size());
backtrack(str,path,used);
return res;
}
void backtrack(string str,string &path,vector<bool>&used)
{
if(path.size()==str.size())
{
res.push_back(path);
return ;
}
for(int i=0;i<str.size();i++)
{
if(!used[i])
{ //之前记录过一次不用再次重复记录
if(i>0&&str[i]==str[i-1]&&!used[i-1])
{
continue;
}
path.push_back(str[i]);
used[i]=true;
backtrack(str,path,used);
used[i]=false;
path.pop_back();
}
}
}
较难
牛客 最长的括号子串
- 栈的方式
时空 O(n) O(n)
int longestValidParentheses(string s) {
// write code here
stack<int>sta;
int last = -1,maxVal = 0;
for(int i=0;i<s.size();i++)
{
if(s[i]=='(') sta.push(i);
else{
//没有(重新确定起始位置
if(sta.empty())last = i;
else{
sta.pop();
maxVal = sta.empty()?max(maxVal,i-last):max(maxVal,i-sta.top());
}
}
}
return maxVal;
}
- 动态规划
牛客 数组中的逆序对
数组前面一个数字大于后面的数字,则为逆序对,求所有逆序对
归并的时候计算
var sum int = 0
func reversePairs(nums []int) int {
sum = 0
Sort(nums,0,len(nums)-1)
return sum
}
func Sort(nums []int,left,right int){
if left>=right{
return
}
mid:=left+(right-left)/2
Sort(nums,left,mid)
Sort(nums,mid+1,right)
merge(nums,left,mid,right)
}
//归并,计算,当前面的数据大于后面则,left剩余的与right当前都为逆序对
func merge(nums []int,start,mid,end int){
var tmp []int
l:=start
r:=mid+1
for l<=mid&&r<=end{
if nums[l]<=nums[r]{
tmp = append(tmp,nums[l])
l++
}else{
sum+=mid-l+1
tmp = append(tmp,nums[r])
r++
}
}
for l<=mid{
tmp = append(tmp,nums[l])
l++
}
for r<=end{
tmp = append(tmp,nums[r])
r++
}
//start 开始的一段数据,不能覆盖nums太多
for i:=0;i<len(tmp);i++{
nums[i+start] = tmp[i]
}
}
牛客 汉诺塔
每个步骤字符串,递归
var res []string
func getSolution( n int ) []string {
// write code here
res=make([]string,0)
move(n,"left","mid","right")
return res
}
// 从left 借助mid到right
func move(n int,left string,mid string,right string){
if n==0{
return
}
move(n-1,left,right,mid)
res = append(res,"move from "+left+" to "+right)
move(n-1,mid,left,right)
}