拖拽碰撞检测算法

1.矩形相交检测算法

两个矩形相交有如下四种情况：

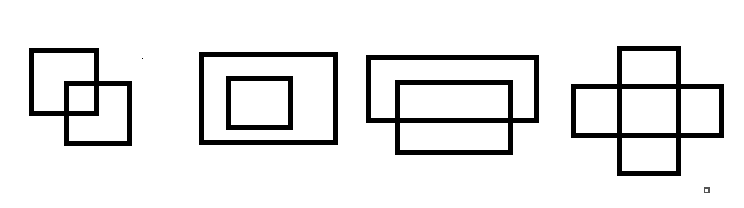
如果两个矩形，假设为o1和o2,若两者相交，那么矩形o1、o2的中心点与矩形的边长是有一定关系的，如下图：

 

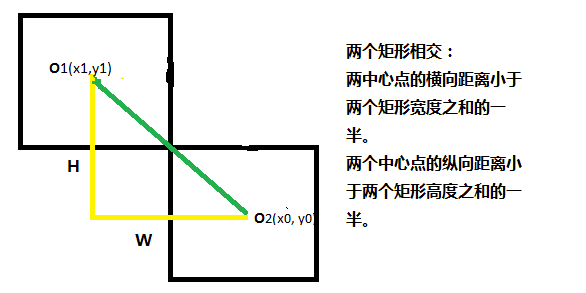
    if(Math.abs(x0 - x1) <= o1.width/2 + o2.width /2 && Math.abs(y0- y1) < o1.height/2 + o2.height /2){
        //相交
    }

如何求相交区域的坐标点？

需要分别获取两个矩形的左上角和右下角的坐标，假设a的左上角坐标点为(left1,top1)，右下角点坐标点为(right1,bottom1); b的左上角坐标点为(left2,top2)，右下角点坐标点为(right2,bottom2)。

假设相交区域左上角的坐标为(x,y)，右下角的坐标为(x1,y1)，那么观察第1张图后可以得出下面的公式：

    //假设横坐标的正轴朝右，纵坐标的正轴朝下
     x = Math.max(left1,left2),y = Math.max(top1,top2); 
     x1 = Math.min(right1,right2),y1 = Math.min(bottom1,bottom2);

2.最近中心策略算法

“最近中心”策略会找到中心距离活动可拖动项的边框中心最近的可拖放容器，宽容度更高。

 

3. 最近角点算法

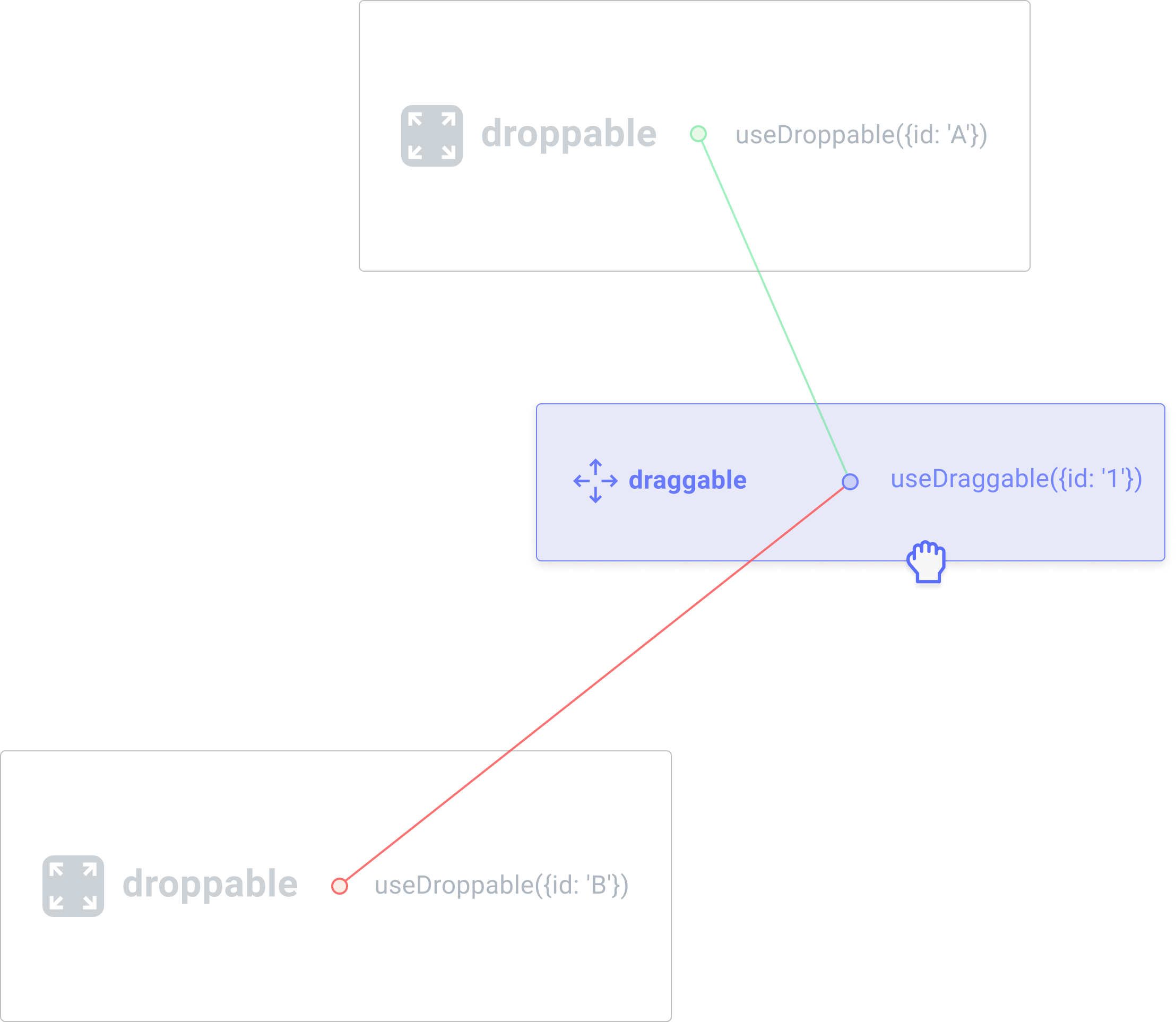
与最近中心算法一样，最近角点算法不需要可拖动和可拖放的矩形相交。

相反，它测量活动可拖动项的所有四个角与每个可拖放容器的四个角之间的距离，以找到最近的一个。